Прибор для вычисления определенных интегралов типа ab f(у) dх

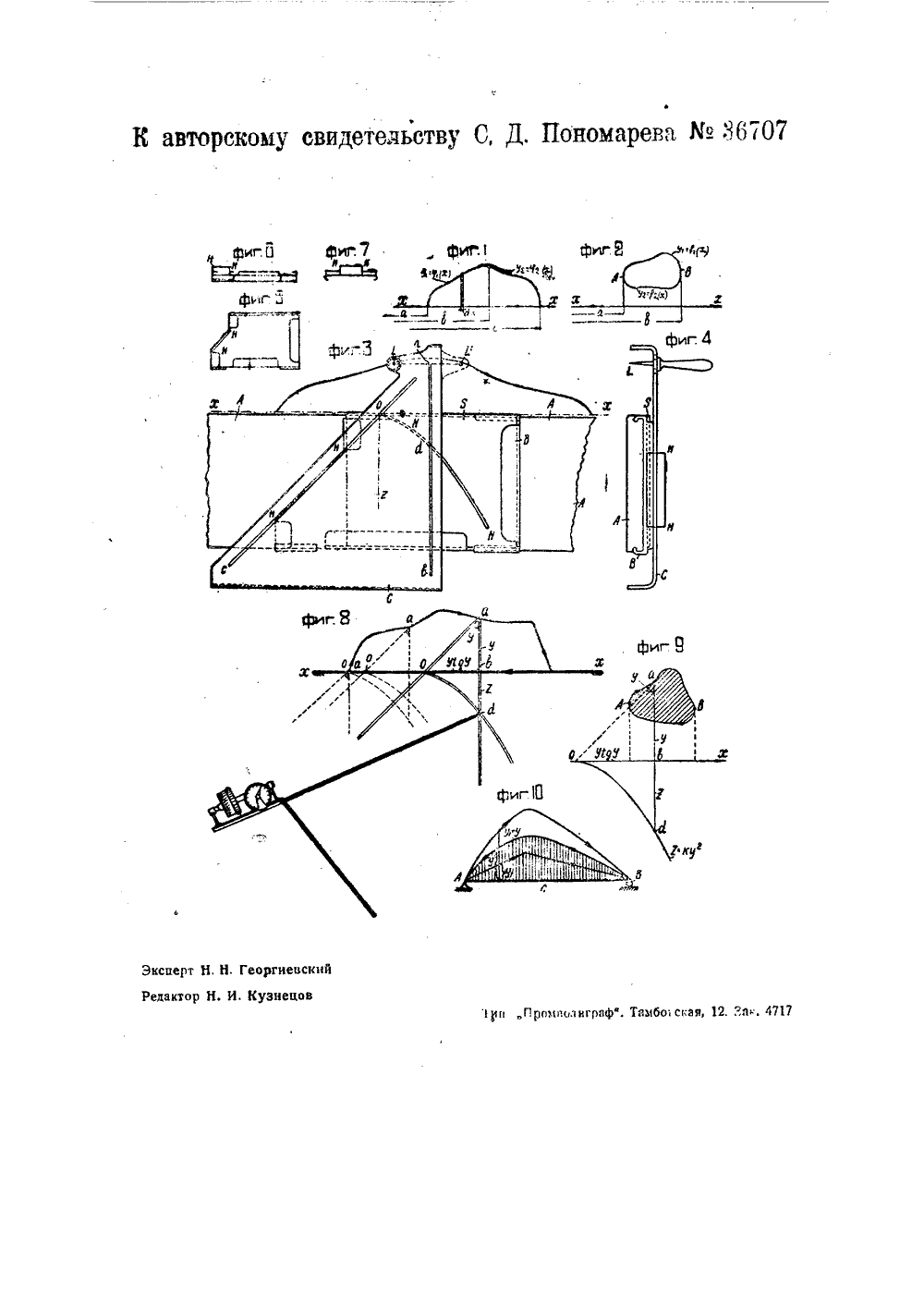
)т),АВТОРСКОЕ СВИДЕТЕЛЬСТВО ИА ИЗО 6 РЕТЕИИЕ О П ИСАНИЕ прибора для вычисленния Определенных интегралов типа /К(и) Жх. аК авторскому свидетельству С. Д. Понамарева, заявлеиноьау 1 июня 19:3 года (спр. о перв. Лп 129625). 0 выдаче авторского сьиаетельства опубликовано 31 абая 1934 го,.а," и,пхРгпхиф,дх ф Ьа ьУ х г г 2 В технике при решении целого ряда практических задач встречается необходимость брать определенные интегралы типаь(у) Их, где у = а) (х).аНапример, при определении стати-, ческого момента Яили момента инер ции Х какой-либо площади относительно оси хх (фиг. 1 и 2) приходится вычислять интегралы: . Если функция у=о(х) задана аналитически, то, во бще говоря, интегрирование может быть выполнено, но обычно это связано с большими математическими выкладками, что требует много времени и умственного напряжения, тем более, что очень часто отдельные участки кривой выражаются разными уравнениями. Не менее часто встречаются фигуры, очерченные линиями, полученными из конструктивных соображений или экспериментально; в этих случаях у =(х) остается аналитически неизве стной, и тогда можно применять только графические способы, которые также требуют много времени и кропотливой работы.Уже с давних пор все проектные организации и научные учреждения снабжены планиметрами, - приборами, позволяющими определять площади фигур, ограниченных любыми линиями.С математической точки зрения можно сказать, что планиметр есть прибор, позволяющий брать определенные интедграды типарых, гда а=т(х):; Ф- ъ,Иь фцфГ 1 редлагаемый.( прибор имеет целью расширить область применения плани метра и позволяет не только брать указанные выше, интегралы, но да.:т воз можность механическим путем вычислять, например, интеграл Мора ж 2 М, Мдх,которйй, как известно,играет громадную роль в теории сооружений, так как с помощью его находятся деформации различных систем.Возможность брать этот интеграл механическим способом значительно упрощает технику расчетов и позволяет внедрить формулу Мора в ряд отделов строительной механики, где до сих пор она применялась лишь в очень слабой степени, в виду сл жности ана литических выкладок, например, в расчет кривого бруса большой кривизны и т. д.На чертеже фиг 1 и 2 поясняют графически определение статического мо. мента 5 или момента инерции lкакой-либо плошади относительно оси хх; фиг, 3 - вид прибора сверку; фиг. 4 - вид сбоку; фиг. 5 - 7 д таль движка в различных проекциях; фиг. 8 - схема, поясняющая пользование прибором, фиг. 9 и Ю - графики, относящиеся к нахождению статического момента .),. и центра тяжес 1 и фигуры относительно оси хх и к определению прогиба балки в некоторойточке ее.Предтагаемый при 5 ор имеет следующее устройство. Вдоль планшайбы А (фиг, 3, 4) может поступательно двигаться движок В, с шаблоном 8, на котором сделан прорез О ЖХ по кривой в=У(у), шириною около 1 мм. Шаблон устроен сменным для того, чтобы можно было применять прибор при различных функциях г =(д),Ось уу у кривой прореза г-= (д) должна совпадать с осью хх заданной кривой и поэтому наиболее удобно, чтобы она помещалась на краю движка (ось ыуу, начало координат точка О),Относительно движка перемещается пластинка С с нанесенным на нейугольником аМ (угол при вершине й равен 45) Одна из сторон угольника асс, представляющая прямой прорез шириною в 3 - 1,5 мм, всегда перпендикулярна к ребру планшайбы А, а следовательно, и к краю движка В и взаимно совмещенным осям хх и уу кри. вой. а=ау). -,Другая сторона угольника асс всегда проходит через начало коордйнат О кривой 3 =(у), в каком бы положении движок В и угольник С йи находились, Для осуществления такой связи между угольником и движком на последнем имеется прямолинейная направляющая НН, проходящая через начало координат О, а сторона угольника . аос представляет собою прорез; таким образом, угольник будет скользить по направляющим относительно дв,",жка с соблюдением указанных выше условий,В вершине угольника а (фиг. 3) помсщается игла, которая для удобства может быть вынесена в сторону параллельно оси Х или Ь. Это будет лишь смещать заданную кривую относительно прибора. Установив неподвижно планшайбу так, чтобы ось уд, совпадающая с краем движка, совмещалась с осью хх заданной кривой, обводят иглой А. или Л заданную кривую по стрелке часов и ось хх справа налево (или наоборот). При эам пластинка С и движок Б перемещаются вдоль плгн- шайоы А, а шпиль планиметра, помещенный в точке И пересечения двух прорезов ЖЛ и аЬ, увлекаемый первым и направляемый последним, будет описывать кривую г Ду)Счетчик планиметра даст намьгах = Ду) дх. Действительно (фиг. 8) иЬ=д. Если р=45, то ад=ОБ=у; если ке сделать угол р не 45, а любой, то ОЬ=у 1 д; иногда это будет лишь менять масштаб и может быть удобно использовано; Ы = г =(у). Шпиль планиметра, связанный с точкой я, будет описывать кривую г=(у), а его счетчик даст нам интересующий нас и нтеграл.На фиг, 8 указано применение прибора, заключающееся в том, что с помощью угольника и шаблона возможноперемешать шпиль планиметра по требуемой кривой без построения этойкривой, и таким образом получать(д) дх, если графически заданод= р гх).Пример 1. Найти статический момент 5 и центр тяжести фигуры (фиг 9)относительно оси хх,Имеем:оЬ = д; ОЬ = д ф= уд, где р = 1 д р.В = Ьд = Л 1 д р дг = Арг д.Установив иглу а в точке А фигуры,записываем отсчет по счетчику планиметра, затем обводим иглу а по контуру фигуры по часовой стрелке; возвратившись в точку А, вновь записываем показания счетчика; разностьконечного и начального показаний даетнам площадь Р фигуры, у которойординаты всехточекравны Лр д,2 2Ях= гд =2 Лух У7 р гПомощью планиметралегко находим- плошадь заданной фигуры.Для того, чтобы найти момент инерции этой фигуры 9 тносительно оси хх,надо воспользоваться другим шаблоном,з :Рдля которого г= - д, тогда l =зрТаким образом мы видим, что определение центра тяжести и моментаинерции любых фигур, т. е, решениедвух больших задач требует всего лишьдвух шаблонов.П ри м е р 2. Особое значение, какуже указывалось выше, прибор приобретает в решении интеграла Мора яЗщ дх, где Л= - (х) и М,=(х)заданы эп юрами изгибающих моментов, например, требуется определитьпрогиб балки в некоторой точке Схг Х 2г ю=;1 ь+цу-Ф-цлф=Х 1 ххг- (д+д,) дх -Хх 2 хг- д,Их -дух2 Г 2х 1 Х 1 т. е,х 2 Х 2ММ,ах=(, +д,)х х 1 хг Хг2 Г 2- д,дх -дКх 1 х 1 Каждый из интегралов, стоящих в квадратных скобках, берется как статический момент с помощью шаблона 2 Г г Рв=lгд, так что ) д дх= - - гдеР площадь эпюры, ординаты которой2 2равны йр д, т. е. ао., (Яу) - 2 1 р г Ф ММ 1 Жс= х 1 о а Зт 2 йр,Движение иглы Ь прибора показанострелками,1) Строим балку в масштабамм -асм,2) Строим эпюру от единичнойнагрузки 1 им -см, т. е. М,=д, 3.3) Строим эпюру изгибающих моментов, откладывая ординаты от оси ххи от единичной эпюры одновременнов масштабе 1 им - см, т, е, М=тд,Сперва, перемещением иглы по часо.вой стрелке,обводится кривая (р+д,1= =у(х), затем кривая р=(х), против стрелки часов, затем ось х слева направо и, наконец, у, =а (х) .и отив стрелки часов. Счетчик планиметра, шпиль которого помещен в криволинейном прорезе, сразу даст нам 2 продР 7гиб = -- О = т 2 (Ф и р могут,2 йрЕУравняться 1).Таким образом, достаточно, не отры. вая руки, обвести иглой прибора кри. вые у+уу и д, и уможить получившуюся плошадь, подсчитанную по планиметру, наи прогиб найден при эпюрах любой сложности, т. е, даже в тех случаях, когда применение общеизвестного правила Верещагина является затруднительным.Совершенно так же решается вопрос об определении деформаций кривого бруса; здесь интеграл Мора имеет видх 1ММ, сЬ и он берется механически, к 1только что описанным способом. Необходимо лишь элюры построить на развертке оси бруса, т. е. дать графически М = в (8) и Л, = У (8).Приведенные примеры показывают,каким образом решаются с помощьюпредлагаемого прибора довольно сложные задачи, которые приходится решать в подседневной инженерной практике. Полная механизация решения ме только сократит математические выкладки и съэкономит много рабочих часов, но прибор позволит передать решение этих вопросов работникам средней квалификации и освободит инженеров от сложных и утомительных подсчетов, которые приходится делать П редмет и зоб ретен ия.Прибор для вычисления олределеньных интегралов типа (у) ах по заданному графически д = р (х), ОтличаюШййсй применением ходящего по план- шайбе А движка 8 со сменным шаблоном 8, на котором имеется прорез ЖЖ по кривой г=Ду) и поверх которого может перемещзться пластинка С с нанесенными на ней в виде угольника прорезами аЬ и ас, из которых прорез аЬ перпендикулярен к ребру план- шайбы Л, и место его пересечения И с прорезом ХУ на шаблоне предназна. чено для помещения шпиля планиметра, а прорез ас всегда проходит через начало О координат кривой г = (у) на шаблоне 8, причем пластинка С снабжена иглой Ь, помещенной в одной из точек прямой, проходящей через вершину а угольника аас параллельно ребру лланшайбы А и служащей для обвода заданной графически кривой.