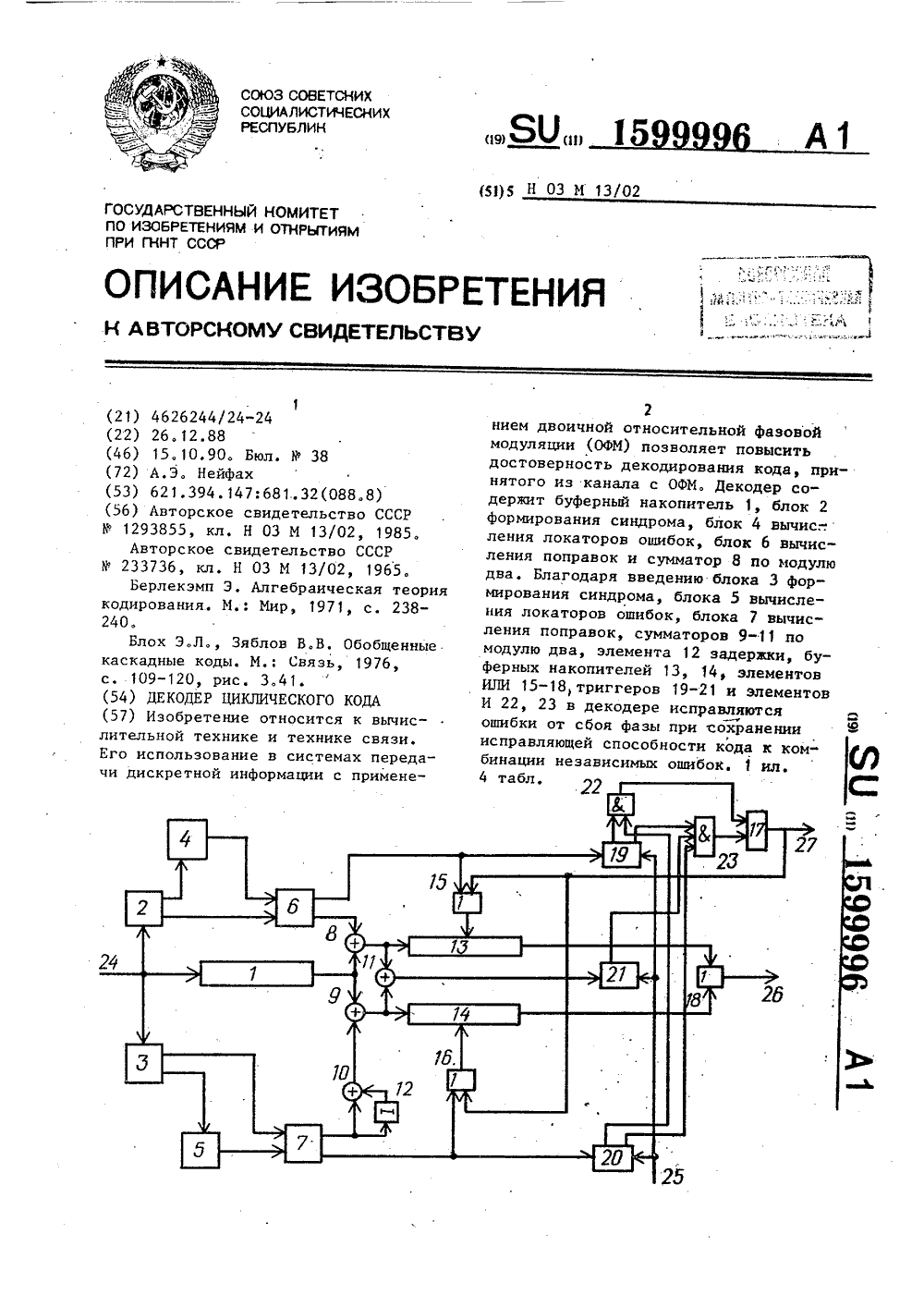
Декодер циклического кода

20 9 1599996 Таблица 3 Результаты этапов декодирования Этапы Многочлен Т(г)=1+в г+, г + ос г +ос г +К 9 г + Ы г,11 0 2 28 3 15 Ф 29 5, .4 6уравнение: С)+а геМ г+Фегг +Ш гф +Н ге)31 г)еС 1 гвод г О12 4 (Ь ) 1+ сс гъо 1+р г+К г 1+о 1 г + К г 73 18 2 19 з 1+ о( г 6 (уход) Пер.к п.7 Пер. к п. 7 Пер. к п. 7 Пер. к п. 11 8 (13, В, с, (К+1 Нет Нет Нет 9 (1), В, с (К+1 1; 1; 0 1; О; 2; 1;(4г 5 О Редактор М,. Товтин Заказ 3151 Тираж 659 ПодписноеВНИИПИ Гос.ударс:твенного комитета по изобретениям и открытиям при ГКНТ СССР 113035, Москва, Ж - 35, Раушская наб д, 4/5 Производственно-издательский комбинат "Патент", г,ужгород, ул. Гагарина,101 Умножение на хОстаток от деленияна многочлен"Матричное умножение" Циклы решения ключевого уравнения (К = 0,1,) 2 3 2х +х +х+1 х+ х +х+1 х+х+х+1 х+х+х+1 Составитель О, РевинскийТехРед М, Дидык Корректор Т. Палий.599996Изобретение относится к вычислительной технике и технике связи и может быть использовано в системах передачи дискретной информации с приме 5нением двоичной относительной фазовоймодуляции (ОФМ).Цель изобретения - повышение достоверности декодирования кода, принятого из канала с ОФМ.1 ОНа чертеже приведена функциональная схема декодера.Декодер циклического кода содержит, первый буферный накопитель 1, первыйи второй блоки 2, 3 формирования синдрома,первый и второй блоки 4, 5 вычисления локаторов ошибок, первый и второйблоки 6,7 вычисления поправок, первый -четвертый сумматоры 8-11. по модулю два,Ълемент 12 задержки, второй и третий буФерный накопители 13,14,первый - четвертый элементы ИЛИ 15-18, первый - третийтриггеры 19-21, первый и второй элементы И 22, 23. На чертеже обозначеныинформационный вход 24, вход 25 обнуления, информационный выход 26 ивыход 27 ошибки.Буферные накопители 1, 13, 14представляют собой регистры сдвига.Элемент 12 обеспечивает задержкусигнала на один такт, т.е. являетсяразрядом такого же регистра сдвига.Блоки 2, 3 формирования синдромавыполнены на основе схем формированияостатка отделения в поле Галуа и метричного умножения в соответствии свыбранными кодами.Блоки 4, 5 вычисления локаторовошибок могут быть выполнены, как впрототипе 4 1,Блоки 6, 7 вычисления поправок40реализуются так же, как в 1 4 , причемна их вторых выходах формируются сигналы, свидетельствующие о наличии неисправимой ошибки,Работа всех указанных блоков тактируется с распределителя импульсов(не показан).В основе работы декодера лежитследующее.Относительная фазовая модуляция получила широкое распространение дляпередачи дискретной информации по каналу связи. Однако применение корректирующих кодов в системах передачидискретной информации затруднено эффектом преобразования одиночных ошибок в двойные смежные, поскольку приОФМ искажение 3-го бита в канале связи вызовет также искажение (3+1)-гобита. Поэтому исправляющая способностьобычного декодера, подключенного навыходе демодулятора, понижается примерно в два раза.Используя введенное в 21 понятиефиктивного кода, который для одинаковых ошибок в канале связи образует теже синдромы при передаче по схеме с11 - иабсолютной модуляцией, какие порождает реальный код при передаче в ОФМ,можно полностью использовать исправляющую способность реального кода,который имеет длину и число информационных символов на 1 меньше, чем со -ответствующие числа для фиктивного1кода, Иначе говоря, возможность исправления ошибок, вызванных сбоями фазыи, одновременно, сохранение исправляющей способности кода для обычныхошибок при передаче сигнала ОФМ можнореализовать, если один и тот же кодиспольэовать для исправления ошибокв двух режимах: в режиме фиктивногокода и в обычном режиме. Эта возможность имеет место для таких кодов,которым соответствуют фиктивные коды,являющиеся циклическими кодами.Для рассматриваемых двоичных кодов21 показано, что циклическому (и,К ) - коду длиной и =, 2 - 1 (здесь9ш - целое число) с минимальным весомс 1, порождающий многочлен которогоу,Р(х) не содержит множителя х+1, соответствует реальный (и, К)-код,и = и- 1, К = К, - 1 с минимальнымвесом Й = с 1, При этом реальным кодомявляется специальным образом укороченЮный циклический код с порождающим многочленом д(х) =8,(х)(х+1) у(и+1,К)кода полной длны с порождающим много"членом ц(х), который ниже будем называть дополнительным кодом, удаленкрайний проверочный символ, а не информационные символы, как у обычныхукороченных циклических кодов.Декодер функционирует следующимобразом,Перед приемом каждого нового кодового слова сигналом со входа 25 триггеры 19-21 обнуляются. Синдром, вычисляемый различным образом в формирователях синдрома 2,3 (соответственно дляреального и фиктивного кодов) при поступлении из канала связи на вход 24кодового слова, используется в блохах4,6, как синдром реального кода, а вблоках 5,7, как синдром фиктивного51599996 6 кода. Поправка, вычисляемая блоком 6, исправленной информации, выделяе прибавляется в сумматоре 8 к информа- сумматором 11, Это позволяет снизу. ции, задержанной буферным накопителем вероятность необнаруженной ошибки в 1 непосредственно а поправка опре- информации в случае появления неиспФ Ф5деленная блоком 7, прибавляется к ин- равляемой комбинации ошибок. формации в сумматоре 10 дважды, по- Рассмотрим особенности функционискольку при ОфМ искажение 3-го симво- рования блоков 2-7 декодеров реальла в канале связи вызовет инвертиро- ного и фиктивного кодов при использование 3-го и Ц+1)-го символов для ванин итеративной процедуры декодиО1-(и) . рования Берлекэмпа, разработанногоЕсли число ошибок в кодовом слове первоначально для обычного цикличесне превышает половины исправляющей кого кода полной длины, Реакльный способности кода, то они могут быть код не является таким кодом, поскольисправлены обеими "половинами" деко 5 ку он получается укорочением дополнидера (2,4,6 и 3,5,7). В накопители тельного циклического кода полной 13 и 14 поступит при этом одинаковая длины. Поэтому для декодирования информация, которая через элемент ИЛИ реального кода можно использовать про подается на выход 26. Данный ва- цедуру декодирования дополнительного риант в случае появления ошибок наи-. кода, у которого крайний проверочный более вероятен, поскольку, ошибки боль- символ будем считать стертым3. шей кратности обычно происходят реже, Алгоритм декодирования реального а вероятность сбоя фазы значительно (п, К)-кода, основанный на алгоритме меньше вероятности обычной ошибки декодирования дополненного (и+1,К)- символа, кода, у которого крайний стертый проЕсли число ошибок будет также не- верочный символ будем считать первым велико, но в канале появится одиноч- по счету, удобно представить в сленая ошибка, вызванная сбоем фазы, то дуюЩем виде. блоки 3,5,7, оперирующие с фиктивнымАлгоритм 11. Вычислить взвешенные степенные большой вероятностью на выходе блока симметрические функции Я , 8 г. а, 8в+0 7 будет сформирован сигнал "Ошибка", от локаторов искажений Я, х. который через элемент ИЛИ 16 произвеи х1=2 дет сброс третьего накопителя 14, Многочлен локаторов стиранийЛ=т 1+х г Происходящий при этом переброс триг, Определить многочлен Т(г) щ гера 20 це приведен к формированиюб 1-35б 1- сигнала "Ошибка" элементами 22, 23 = 1 + Тг(1+ .Е.За Л. и 17, если не будет переброшен тригк: гер 19, Блоки 4 и 6 произведут в сум Решение ключевого уравнения маторе 8 исправление ошибок вместе сыошибкой фазы и исправленная информа " К - 0о из 1 сф1,0(0) = О,Уция из накопителя 13 поступит на вы- В(0)0 - исходные данные. ход 26 к потребителю.4. Определить Л., - коэффициент прикЕсли число ошибок кодового словапревысит половину исправляющей спо ев многочлене (+,Е.Т )% (Ъ) . собности кода, но не превзойдет пг последнюю, то блоки 4 и 6 не смогут 5. Вычислить"," = + Ь",г(, " исправить последовательность ошибок 6. Т известно Нет - пер.11.сформированный с большои вероятно 7 Е , тз О 1(К)11 истью сигнал Ошибка на выходе блока-.12б произведет сброс накопителя 13, а реет бдд,Гр(к) + 1 б бцб) О исправленная информация с накопителя. 2 3 14 поступит на выход 26. где, то - пер.8. иначе - пер.Я.Одновременный сброс накопителей8. 1)(К+1)=11(К) р В(К+1)=В(К)13 и 14 и формирование сигнала шиб- ъ 11= з 1;. Пер.10. ка" на выходе элемента ИЛИ 17 прои 9. Р(К+1)К+1 - П(К); В(К+1) зойдет в декодере в двух случаях:если сигнал "Ошибка" возникает в обо- , Й,( их блоках 6 и 7 - через элемент И 22, - 10, К, = К+1 Пер4.и при появлении сигнала несовпадения Вычисление и исправление ошибок. При этом раздел алгоритма 1 "Решение ключевого уравнения" (блоки 3- 20 10 алгоритма) реализуется в блоке 4 декодера, а раздел "Вычисление и исправление ошибок" (блоки 11-20) алгоритма - в блоке 6 декодера.Рассмотрим особенности выполнения 25 блока 2, в котором реализуется блок 1 алгоритма 1, Для декодирования обычных циклических кодов по процедуре Берлекэмпа степенные симметрические функции Б вычисляются следующим об О разом.1. Производится вычисление остатка от деления принятого кодового слова к(х) на минимальный многочлен М(Ы) элемента расширенного поля Галуа 0.352, Выполняется преобразование остатка в соответствии с процедурой "матричного умножения" (поясняется ниже на примере).Для рассматриваемого реального кода, не являющегося циклическим, эта процедура требует модификации, которую только для удобства изложения рассмотрим на примере простейшего реального (6,3)-кода, для которого 45 К - корень неприводимого многочлена Одновременно, только для этого примера порождающий многочлен фиктивного (7,4) - кода я (х) = хд + х + 1. Проверочная матрица дополненного (7,3) - кода имеет вид50н Ы МЫ ЫФЫоп 1 1 1 1 1 1 1 .101110 0011100 О111111 1К подматрице матрицы (1) размерности 6 х 3, отмеченной пунктиром, следует привести проверочную матрицу реального кода с целью применения блоков 3-20 алгоритма 1 декодирования. Поскольку линейная операция над строками проверочной матрицы линейного кода приводит также к проверочной матрице, то сложение последней и предпоследней строк матрицы 1 для удаления правой "1" в предпоследней строке приведет также к проверочной матрице дополненного кода, удаление правого столбца и нижней строки которой приведен к матрице реального кода 101110(2) Н = 111001 Р 100011 Матрица (2) отличается от выделенной подматрицы матрицы (1) только инверсией нижней строки, поскольку нижняя строка "единиц" матрицы (1) является проверкой на четность, Для того,чтобы получить необходимые для декодирования степенные симметрические функции 81 в виде линейных комбинацийстолбцов выделенной подматрицы матрицы (1), нужно в процедуре вычисленияфункций Б просто повторить вышеприведенные операции с матрицей Н 4 иДопполучится процедура вычисления степенных симметрических функций Яв следующем виде.Процедура 2,1. Умножение многочлена принятогокодового слова на "х" (с цельюприсоединения" отброшенного символа дополненного кода)2. Получение остатка от деленияна минимальный многочлен М(п"),3. Вычисление четности, например,делением на двучлен (х+1).4. Добавление четности по п. 3к младшему разряду остатка по п,2.5. Если остаток не равен 0 и четность равна 1, то - инверсия младшего разряда остатка (модифицированногопо п. 4).6. Преобразование результата процедурой "матричного умножения".Проиллюстрируем применение алгорит. ма 1 и процедуры 2 в полном объеме.на примере реального (30, 15) - кода,которому соответствуют фиктивный(31, 16)-код, имеющий минимальныйвес йд = 7 и дополненный (30,15)-кодс дщ = 8 с проверочной матрицей9 1599996 106 за 27 агв 27 гб г 5 24 гз гг г га ч о 7 б 15 14 з 2 а 4 ь 7 б 5з ггз 27 25 гз г 19 1 а 5 з , 9 7 5 з зо гв гб г 4 гг,гаввов 4 2 а в 6 4 г 128 25 22 9 1 б З 1 О 7 429 7 гб 2 З 20 17 Ф 11 Ь 5 1За 2724 г Во 15 Р 244 б Зк о27 гз 9 151 7 з зо, 26, 22 ь 1 ов 76 72 29 25 ого 7 озо 9 оьКо а 7. 7 Д о о. о О26 21 16 1 6 27 22 7 2 7 2 26 23 8 1 з 8 озо 2 ого 9414698 ф з оБ Ю Ы о 1 Г25 ч з 7 26 го 4 8 2 27 21 15 9 Ь гв 22 6 о 4 29 гз 797 обо 8 озоб 24 осво 6 940 1 1Ф 4 4 4 1 1 1 4 1 1 1 1 1где (для этого примера) с 4, - кореньминимального многочлена М(ЬД =х +х +1.- 6 2Кодирование следует производить путемприписывания к передаваемой информационной части слова п - К + 1 = 16 15нулей, деления на порождающий многочлен реального кода я (х)х + х +16 1+ х г+ х 7 + х + х+ х 4 + 1, отбра 1 Х 7 б 5 Р Фсывания младшего проверочного разряда(степени х ) и вывода оставшихся 20и-К = 15 символов в качестве проверочной части кодового слова. Многочленд (х) =, (х+1).ят(х), где я, (х) - по-.рсждающий многочлен фиктивйого кода,д(х) = И(оС) М(М ) М(с 2 ), в которомМф( з) с+ 4 + 3+ г+М Ыа) =х чх +х +х ч 1. Отметим, что элементы 2-ой, 4-ой и 6-ойстрок матрицы (3) являются четнымистепенями соответственно элементов 301-ой и 3-ей строк, не нужны для определения кода данного примера и включены в матрицу (3) лишь для удобствапояснения процесса декодирования.Степенные симметрические функцииБ 1, определяемые в п. 1 алгоритма 1,представляют собой сумму элементов1-и строки матрицы (3), соответствующих искаженным при приеме символамкодового слова,Для нахождения степенных функцийприменимпроцедуру 2, в пунктах 1-5которой для Б, Б, Б 4 будет использоваться г (ЬО - остаток от делениянаМ(Ф) = х + х + 1, для БЬи Бб 45(3)г , Ы з) - остаток о т деления н а М (,в )и для Б- соответственно г ( о ) ,ЮВ процедуре матричного умноженияпо и. б матрица, используемая дляполучения Б 4, оказывается единичной,поэтому Б 4 просто совпадает с "пятибитом" (для данного примера), полученным в п. 5. Однако, вычислениеБг - Б требует более сложной схемы,Схемы связи для этих матриц умноженияполучаются из правых пяти столбцоврасширенной матрицы Н (3), в которойстолбцами показаны двоичные (пятиразрядные) эквиваленты элементов Ы 1 1 1 ( 9 11 1 4В табл. 1 показаны матрицы умножения для 6-го этапа процедуры 2 вычис,ления степенных сумм Б 1 - Б б.Благодаря такому выполнению по п.1 алгоритма 1 проверочная матрица реального кода для целей декодирования получается в виде отмеченной пункти-, ром части матрицы (3), т.е. беэ столб. ца и строки, состоящих их единиц,В табл, 2 представлены результаты этапов выполнения процедуры 2 вычисле-" ния функций Б при искажении в принимаемом кодовом слове 5-го символа справа (степени х , поскольку в прканимаемом кодовом слове правый бит соответствует нулевой степени многочлена) .В табл, 3 приведены результаты этапов решения ключевого уравнения для реального кода по алгоритму 1 при искажении в принимаемом блоке первого и второго символов справа (х+1).В результате решения ключевого уравнения алгоритм 1 в данном примере переходит к п 11 с ф (г)=1+фэг + + оЗС = (1+ Ог)(1+ Ог.г). Дальнеишее выполнение алгоритма 1 приводит к исправлению двух ошибок при следующей последовательности операций с указанием их результатов в угловых скобках12 С 1=1 3; 13 с )(Ы= 0;16 с Ъ(г) = 1+ Фгг ; 17; 18; 13сЪ (О") 76 0); 14,1=2); 15; 13(с(0) = 01; 16( (г)=1); 17; 18;1 У.Для рассмотрения принципов работыблоков 3,5,7 при декодировании фиктивного кода вернемся к простейшему примеру реального (6, 3)-кода, для которого желательный (в целях удобства декодирования) вид матрицы фиктивного (7, 4)"кода будет матрица (1) без ниж. ней строки единиц. Если воспользовать-. ся формулами преобразования проверочной матрицы фиктивного кода в проверочную матрицу реального кода3 ,1,1Ь а + Ь (1 2-и) (5)фг 1Ф11.159999612т11где а , Ь - соответственно 1-е столб- в процедуре вычисления функций повтоцы проверочной матрицы реального и рить приведенные операции для полу- фиктивного кодов (при этом, имеем так- чения матрицы (8) и получится процеже соотношение для матрицы фиктивного дура вычисления степенных симметрич 51 кода ных функций Б в следующем видеи+с. Ь 0 ) (6)Процедура 31-( 1. Умножение многочлена принятогокодового слова на х.2. Получение остатка от деления намногочлен (х+1) М(К).3. Удаление младшей компоненты остатка (степени х, уменьшение на 1степеней остальных компонент остатка.4. Выполнение преобразования полученного синдрома (остатка) Бюв- (Ь (9)1 11 20 1 последовательно, с ростом 1, где и) - , степень минимального.многочлена М)(. ).35, Преобразование результата процедурои матричного умножения" аналогично процедуре 2.Вычисленные с помощью процедуры 3 симметрические функции могут быть использованы для обычной итеративной Например, из верхней части матрицы (1) получим проверочную матрицу реального кода 25 110 10 Н =- 101 11(8) НР где 0 - пулевой вектор) и если матрица фиктивного кода представлена в 10каноническом виде, т.е. правая подматрица размерности (п-К)(и-К) представляют собой единичную матрицу 1 ,то в правой части матрицы реальногокода получим после преобразования (5) 15подматрицу вида Поскольку линейное преобразование над строками проверочной матрицы линейного кода приводит также к проверочной матрице, то в матрице (7)можно заменить вторую строкусуммой первой и второй строк, .а затем 35 третью строку - суммой трех строк. В результате получим проверочную матрицу в каноническом виде С другой стороны, 1-й столбец матрицы (8) можно получить с помощью 45 следующей процедуры:1. Приписывание Оп справа к принятому слову (умножение многочлена принятого слова на "х");2. Получение остатка от деления на многочлен ц (х) = д(х) (х+1) = =(х + х + 1) ф(х+1)=х + х, + х + 1.3. Удаление младшего символа остатка.Для того, чтобы получить необходимые для декодирования в фиктивном коде степенные симметрические функции 81 в виде линейных комбинаций столбцов верхней подматрицы матрицы (1), нужно процедуры декодирования, в частности,может быть испольэован,приведенныйвыше алгоритм 1, в котором операция12 заменена следующей: "12.:=0",алгоритм 1 со скорректированной операцией 12 назовем "Алгоритм 1 а".Проиллюстрируем применение процедуры 3 и алгоритма 1 с) в полном объемена примере реального (30, 15)-кода,которому соответствует фиктивный(31,16)-код, имеющий проверочную матрицу (3) с удаленной нижней строкойединицПусть на блок 3 поступает нулевоекодовое слово с искаженным пятым ишестым символами справа (двучленх + х ). В табл, 4 представлены реьзультаты .этапов выполнения процедуры3 вычисления функций Б ,Отметим, что на этапе 2 процедуры3 вычисляются остатки от деления намн(1 гочлен (х+1) М)(.) = хб + х + х += х + х + х + 1 для 1:-ой строкиматрицы (3) .Вычисленные значения образуют вматрице (3) шестой столбец справа,который породит единичный импульс исправления с декодирующего выхода блока 7, но на выходе сумматора 10 из(10) 13 159 за задержки в элементе 12 будут сформированы сигналы для исправления двух соседних символов.Отметим также, что процедура 3 мо- жет быть упрощена за счет совмещения операций 4 и 5, поскольку преобразование синдрома по формуле (8) может быть выполнено методом "матричного умножения" на матрицу преобразований 9996 14исправляющего ошибки только вфиктивном коде при условии отсутствиясбоев фазы в кодовом слове.Обозначим через Р вероятностьневозможности декодирования слова,пораженного ошибками символов, приусловии отсутствия сбоев Фазы в кана"ле, под этим будем понимать как отказ 10от декодирования, так и ошибочное декодирование. Через Р обозначим ве-роятность сбоев фазы в слове. Ввидунезависимости искажений символов исбоев фазы вероятность невозможностидекодирования в 12 будетзхххх 1 Согласно математическому определению матрицы последовательное выполнение двух матричных преобразований можно заменить одним преобразованием в соответствии с матрицей - произведе нием двух частиц.В качестве примера для оценки зф-фективности изобретения рассмотрим двоичный (63, 33)-код, порождающий многочлен которого не содержит умно- жителя х+1 (злемент показателя 0 не является корнем многочлена) и минимальный вес которого д11. Такой ход может быть фиктивным (п = 63), а реальный (62, 32)-код, у которого и, = 62, также имеет ди= 11 и может исправлять до Т = (с 1 ми -1)/2=5 ошибок.По фиктивному коду декодер (блоками 3,5,7) исправляет до 5 ошибок битов, но без сбоя фазы. По реальному коду декодер (блоками 2,4,6) может исправлять не более двух ошибок символов, поскольку каждое искажение ошибочного символа в канале дает в результате сдвоенную ошибку в приемнике ОФМ. Однако, декодер по реальному коду может в кодовом слове длиной 62 бита исправлять одну ошибку фазы и до двух ошибок символов или 2 ошибки фазы и одну ошибку символа (пренебрежем появлением большего числа сбоев фазы в слове, чем лишь занизим исправляющую способность декодера) .Пусть в канале вероятность искаже 1 ния символа Р, см=5 10-, а вероятность сбоя фазы на данном символе Р фаз = - 10 , причем искажения символов и сбоев фазы распределены случайно и независимо друг от друга. Рассмотрим сначала возможности декодера аналога% Р = 1 - (1-Р )(1-Р,), (11)где Р = 1-(1-Р,р ) Р (12),Ф 3Для вычисления Ря удобно воспользоваться формулойнРи + ав которой достаточную точность расче та можно получить при использованиипервых четырех слагаемых по знаКамсуммы, С, = 5.Для данного примера Р = 000618,а Р нс = 05826 10е из значительногопревышения Рр над Р, видно, чтоисправляющая способность кода недоиспользуется за счет невозможности исправления в прототипе сбоев фазы. Поскольку Р 7 Рнс, подстановка этихзначений в (11) даст Ри = Рр= 0,00618Для предложенногодекодера сцелью учета рассмотренных выше возможностей блоков 2,4,6 из рассчитанной величины Р следует вычесть поправку Рс, формула для которой получается в виде1 -1Расчет по формуле (14) даст ЬРс= 0,00002 показывает, что верхняя:оценка вероятности ошибочного декодирования предложенного декодера по-.лучается для параметров. данного при мера на 2,5 порядка ниже, чем для аналога 12 .Теперь предположим, что в декодерециклического кода прототипа Я реализован рассматриваемый (63,33)-код15 ,599996 Боуза-Чоудхури. Ксд может гарантированно исправлять= 2 пары ошибок, но исправлять 3 пары ошибок в общем случае не может.5Подставляя в формулу (13) значения и = 63 и Т = 2 вместо соответственно п и С, получим для прототипа при использовании первых двухI слагаемых под знаком. суммы величину Р н = 0,00385, которая заведомо меньше результата использования всех слагаемых формулы (13), но значительно больше оцененной выше величины Р предложенного декодера, 15 Формула изобретения Декодер циклического кода, содержащий первый буферный накопитель,вход которого объединен с входом первого блока формирования синдрома иявляется информационным входом декодера, первый и второй выходы первогоблока формирования синдрома подключены соответственно к первому входу 25первого блока вычисления поправок ик входу первого блока вычисления локаторов ошибок, выход которого соединен с вторым входом первого блокавычисления поправок, первый выход которого и выход первого буферного накопителя подключены к первому и второму входам первого сумматора по модулю два, о т л и ч а ю щ и й с ятем, что, с целью повышения достоверности декодирования кода, принятогоиз канала с относительной фазовой модуляцией, в декодер введены второй итретий буферные накопители, второй -четвертый сумматоры по модулю два,элемент задержки, первый - третий40триггеры, первый - четвертый элементыИЛИ, первый и второй элементы И, второй блок вычисления локаторов ошибок,второй блок вычисления поправок ивторой блок формирования синдрома,вход которого подключен к информацион. ному входу декодера, а первый и второй выходы соединены соответственно 16с первым входом второго, блока вычисления поправок и входом второго блока вычисления локаторов ошибок, выход которого подключен к второму входу второго блока вычисления поправок, первый выход которого непосредст- венно и через элемент задержки соединен с первым и вторым входами третьего сумматора по модулю два, выход которого соединен с первым входом вто- рого сумматора по модулю два, второй вход которого подключен к выходу пер вого буферного накопителя, вторые выходы первого и второго блоков вычисления поправок подключены к установочным входам одноименных триггеров и первым входам одноименных элементов ИЛИ, выходы которых соединены с входами обнуления соответственно второго и третьего буферных накопителей, выходы которых подключены к первому и второму входам четвертого элемента ИЛИ, выход которого является информационным выходом декодера, входы обнуления первоГо - третьего триггеров объединены и являются входом обнуления декодера, первые выходы первого и второго триггеров подключены к первому и второму входам первого элемента И, выход которого соединен с первым входом третьего элемента ИЛИ, выходы первого и второго сумматоров по модулю два подключены к информационным входам соответственно второго и третьего буферных накопителей и соответственно к первому и второму входам четвертого сумматора по модулю два, выход которого соединен с установочным входом третьего триггера, выход которого и вторые выходы первого и второго триггеров подключены к первому - третьему входам второго элемента И, выход которого соединен с вторым входом третьего элемента ИЛИ, выход которого подключен к вторым входам первого и второго элементов ИЛИ и является выходом ошибки декодера.(для 8 ) б 1 0 1 0 1 0 0 0 1 1 1 1 0 1 0 0 1 1 1 0О 01. 1 4 З 2 х х х х х х 1 х 1 Таблица 2 Яз Ф У 86вш щМ а Этапы процедуры 2 х хфхЬ Умножение на "х" х 5 Остаток от деленияна М(О х +1 х +х +х+1 х +х +х +1Ф 2 Ф 3 2 4 Ъ 2 г.х. +1 х +х +х + х +После инверсиимладшего разряда х +1 4 + З+ 4 фО + 4 ОС+1 = Ь(+ЬС.ЬЕ г Э 7 ЙО+1= ЫК еФ+4ы Результат матричного перемножения Ф +ОфМ Ы +1=Ы Ф, 11 с 1 О0 К 0 1 01 р О ыы10 4 0К 10