Способ определения девиации курсоуказателя подвижного объекта
Формула | Описание | Похожие патенты | МПК / Метки | Текст | Заявка | Код ссылки
Номер патента: 1822248
Авторы: Проскуряков, Саюров, Скрипкин
Формула
СПОСОБ ОПРЕДЕЛЕНИЯ ДЕВИАЦИИ КУРСОУКАЗАТЕЛЯ ПОДВИЖНОГО ОБЪЕКТА по авт. св. N 1633930, отличающийся тем, что, с целью обеспечения возможности определения девиации на подводных лодках, оборудованных размагничивающими устройствами, после проведенных измерений включают размагничивающее устройство, в одном из курсовых положений вторично измеряют нормальную составляющую напряженности магнитного поля объекта, углы крена и дифферента, по которым находят продольную, нормальную и поперечную составляющие магнитного поля размагничивающего устройства, с учетом которых находят результирующие продольную, нормальную и поперечную составляющие магнитного поля объекта.
Описание
Целью изобретения является обеспечение возможности определения девиации на подводных лодках, оборудованных размагничивающими устройствами.
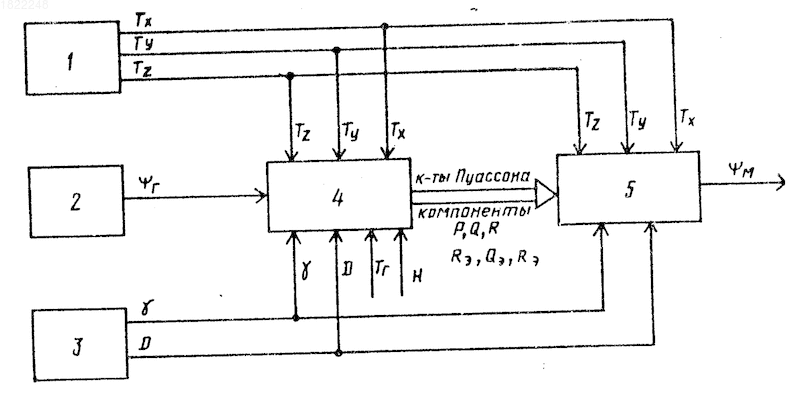
На чертеже приведена структурная схема устройства для осуществления предложенного способа.
Устройство для осуществления способа содержит блок из трех ортогональных жестко закрепленных на корпусе объекта магнитометров 1 для измерения проекции продольной Тх, поперечной Тz и нормальной Тvсоставляющих вектоpа напряженности результирующего магнитного поля объекта на оси связанной системы координат OXYZ, гироскоп 2 направления для определения гироскопического курса
Соотношения для определения магнитного курса подвижного объекта основываются на следующих теоретических положениях.
Магнитные девиации магниточувствительных датчиков обусловлены наличием собственного магнитного поля носителя, на котором они установлены, а геометрические девиации обусловлены изменением ориентации подвижного объекта относительно геомагнитного поля, причем структура собственного магнитного поля объекта такова, что оно содержит постоянную и переменную составляющие. Постоянное магнитное поле носителя определяется наличием на носителе элементов из магнитомягких и магнитотвердых материалов, характеризуемых магнитной восприимчивостью к внешнему магнитному полю (намагничиваемостью в технологических и эксплуатационных условиях). Эта составляющая напряженности магнитного поля носителя
Переменное магнитное поле носителя
индуктивного поля магнитных масс
магнитного поля электронагрузок
магнитного поля вихревых токов
магнитного поля двигателей
Напряженность результирующего магнитного поля носителя T
Превалирующую роль в формировании магнитного поля носителя обычно играют три первые составляющие (причем
Т Т +
S
(4) А матрица ориентации системы координат, связанной с объектом ХYZ относительно горизонтальной геомагнитной системы координат.
Коэффициенты Пуассона и компоненты постоянного магнитного поля подвижного объекта находим следующим образом.
Предположим, что имеется не менее четырех результатов экспериментов, проведенных при четырех различных стояночных курсов
(S+T) (Ai-Aj)
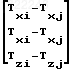 (i,j=1,4)
(i,j=1,4)(5)
Разностные уравнения (5) должны удовлетворять непрерывному условию i
Системе трех разностных уравнений вида (5) соответствует система девяти разностных уравнений Пуассона следующего вида:
(a + 1) (ai aj) + b(bi bj) + c(ci cj)
TXi TXj
d(ai aj) + (e + 1) (bi bj) + f(ci cj) TYi TYj;
g(ai aj) + h(bi bj) + (K + 1)(ci cj) TZi YZj
(i,j 1,4) (6) где ai, aj, bi, bj, ci, cj функции, определяемые зависимостями от составляющих Тг, Тв вектора Т и углов ориентации подвижного объекта
ai Tг
bi= Tв
сi Тг(cos
sin
Систему девяти скалярных уравнений вида (6) можно привести к матричной форме:
N квадратная матрица размером (9х9) с элементами
aij=(ai-aj); bij=(bi-bj); cij=(ci-cj); (i,j=
Матрица N для системы девяти уравнений вида (6), соответствующая варианту трех экспериментов типа (1-2) (1-3) (2-4) имеет следующий вид:
N

(10)
Матрица N является неособенной, так как не содержит линейно зависимые строки и столбцы. Для нахождения обратной матрицы N-1детерминант матрицы N может быть определен по стандартной программе, например, приведением матрицы N к форме Фробениуса (диагонализация матрицы) с последующим определением произведения элементов главной диагонали.
Окончательно детерминант матрицы N имеет вид:
D1 det[N] (a1-a2)2
x (b2-b3)2
Решая далее уравнение (8) относительно
Раскрывая решение (12), используя формулы Крамера, находим следующие выражения для определения коэффициентов Пуассона и составляющих вектора постоянного магнитного поля носителя:
a
d
f
K
(13) где Fi(i=
F1= [c
F2=[tg
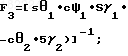 5
5 F4=[c
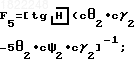 -c
-c F6=[s
F7= [c
F9=[s
где Т1 (ТХ1 ТХ2), Т2 (ТY1 TY2) T1.
T3 (TZ1 YZ2) T2;
T4 (TX1 TX3) T3, T5 (TY1 TY3) T4
T6 (Tz1 YZ3) T5
T7 (TX2 TX4) T6, T8 (TY2 TY4) T7,
T9 (TZ2 TZ4) T8 (15)
После определения коэффициентов Пуассона составляющие вектора постоянного магнитного поля носителя определяются следующим образом, запишем матричное уравнение Пуассона (3) в виде
(16) отсюда в скалярном виде алгоритмы определения составляющих вектора постоянного магнитного поля носителя принимают вид:
Р ТХ1 (a+1)
Напряженность магнитных помех оси ферромагнитных масс объекта может превышать по модулю вектор Т напряженности геомагнитного поля. При этом магнитные девиации магниточувствительных датчиков курсовых систем могут достигать несколько десятков градусов (1, 2, 4).
Преобразуем матричное уравнение Пуассона (3) к следующему виду:
(18) где Тх, Тy, Tz проекции вектора
E единичная матрица размеров (3х3);
Тг, Тв горизонтальная и вертикальная составляющие геомагнитного поля;
Tв=Z=T
(19)
А [aij]33 матрица направляющих косинусов,
где
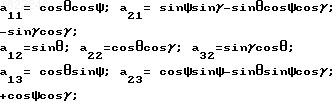
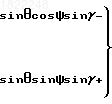
обозначим s sin; c cos
Из теории и практики измерения магнитных девиаций известно, что коэффициенты Пуассона (а, b, k) и составляющие постоянного магнитного поля объекта
Матричное уравнение (18) приведем к скалярному виду:
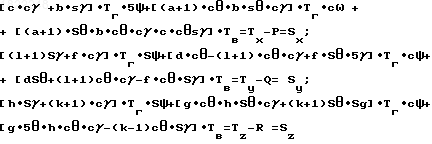
Введем следующие обозначения:
Тг
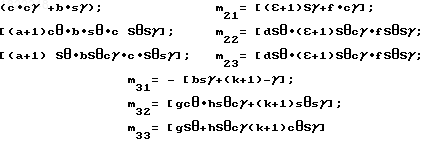
Cистему уравнений (21) сведем к матричному виду:
M
М квадратная матрица размером (3х3)
SX TX P; SY TY Q; SZ TZ R (24)
Решая уравнение (11) получим
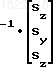
(25)
М-1 обратная матрица
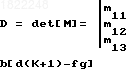
(26)
По формулам Крамера:
Tгc
(27)
Введем вспомогательные функции:
L1 dh g(e+1), L2 gf d(a+1);
L3 bg h(a+1);
L4 cg (a+1)(K+1),
L5 bg (a+1)(e+1),
L6 cd f(a+1)
L7 hf (e+1)(K+1), (28)
L8ch b(K+1)
L9 bf c(e+1)
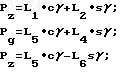
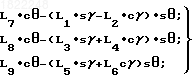
В итоге соотношение для нахождения магнитного курса запишется в следующем виде:
K1=
Однако на ряде объектов (например, на надводных кораблях различных классов, подводных лодках (ПЛ) для компенсации компонент постоянной составляющей МПО используют различные виды размагничивающих устройств (РУ). В зависимости от характера распределения ферромагнитных масс на объектах собственное МПО предъявляется в виде одно, двух, трех- или n-дипольной модели и требует для своей компенсации от трех до 9.11 размагничивающих обмоток, устанавливаемых в различных сечениях корпуса ПО и задействованных постоянно при выполнении объектом боевой задачи, сила тока в которых изменяется в зависимости от изменения курса объекта и его местонахождения (2).
Предполагая, что задача идентификации МПО с учетом работы РУ может быть решена в два этапа:
1. определение коэффициентов Пуассона (а, b,k) и компонент (Р,Q,R) с выключенным РУ;
2. определение компонент электромагнитного поля Р3, Q3, R3формируемого РУ, с учетом известных уже параметров Р, Q, R и элементов матрицы [S] покажем решение задачи идентификации МПО на втором этапе. Для этого запишем уравнение Пуассона (18) в векторно-матричной форме с учетом работы РУ:
(33) где Рэ, Qэ, Rэ компоненты электромагнитного поля, формируемого РУ.
Преобразуем уравнение (33) к следующему виду:
(S+E)
(34)
Умножая матричное уравнение (34) слева на обратную матрицу (S + E)-1 получим
 + A
+ A (35)
Найдем обратную матрицу (S + E)-1 матрица D (S + E) имеет вид:
D
(36) ее миноры:
A11=
A12=
A13=
A21=
A22=
A23=
A31=
A32=
A33=
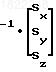
Алгебраические дополнения:
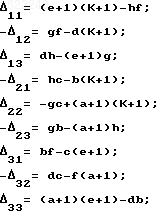
(38)
Детерминант матрицы Д:
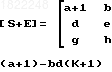 +1
+1 (39)
Тогда обратная матрица D-1 имеет вид:
D-1= [S+E]-1=
(40)
Раскрывая уравнение (35) с учетом выражения (40), получим:
Pэ=
Qэ=
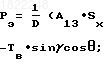 +A23
+A23 Sx=p-Tx; Sy= Q-Ty; Sz=R-Tz;
Далее преобразуем уравнение (33) к следующему виду:
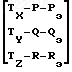 + S
+ S (42)
В скалярной форме:
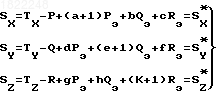 (43)
(43)Производя преобразования, аналогичные выполненным ранее соотношениям (21-27), в итоге получим следующее выражение для определения магнитного курса ПО с включенным РУ:
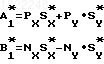
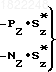 (45)
(45)K1=
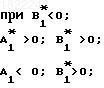 (46) где РХ, PY, PZ, NX, NY, NZ определяется из соотношений (28, 29).
(46) где РХ, PY, PZ, NX, NY, NZ определяется из соотношений (28, 29).В процессе предстартовой подготовки объект с не включенным РУ последовательно устанавливают в четырех различных курсовых положениях, в каждом из положений в первый вычислитель 4 поступают значения продольной ТXi, нормальной ТYi и поперечной ТZi составляющих векторов напряженности результирующего магнитного поля объекта с блока 1, угла курса
В качестве датчиков блока 1 могут быть использованы, например, феррозондовые датчики, в качестве блока 2 и блока 3 могут быть использованы, например, гидроагрегат ГА-8 и гировертикаль МГВ-2 соответственно.
Первый вычислитель 4 и второй вычислитель 5 могут быть реализованы, например, на стандартных элементах вычислительной техники.
Изобретение относится к магнитному курсоуказанию и навигации, предназначено для использования на подводных лодках и является усовершенствованием известного способа, описанного в авт. св. СССР n 1633930. Цель изобретения - обеспечение возможности определения девиации на подводных лодках. Способ основан на том, что включают размагничивающее устройство и в одном из курсовых положений вторично измеряют нормальную составляющую напряженности магнитного поля объекта, углы крена и дифферента, по которым находят продольную , нормальную и поперечную составляющие магнитного поля размагничивающего устройства, с учетом которых определяют результирующие продольную, нормальную и поперечную составляющие магнитного поля объекта. 1 ил.
Рисунки
Заявка
4873869/10, 17.08.1990
Конструкторское бюро промышленной автоматики, Саратовский политехнический институт
Проскуряков Г. М, Скрипкин А. А, Саюров В. Д
МПК / Метки
МПК: G01C 17/38
Метки: девиации, курсоуказателя, объекта, подвижного
Опубликовано: 20.01.1996
Код ссылки
<a href="https://patents.su/0-1822248-sposob-opredeleniya-deviacii-kursoukazatelya-podvizhnogo-obekta.html" target="_blank" rel="follow" title="База патентов СССР">Способ определения девиации курсоуказателя подвижного объекта</a>
Предыдущий патент: Пуансон для формовки обтяжкой
Следующий патент: Обойма надбандажного уплотнения регулирующей ступени паровой турбины
Случайный патент: Устройство для резки трубчатых изделий