Роторная машина (ее варианты)
Формула | Описание | Похожие патенты | МПК / Метки | Текст | Заявка | Код ссылки
Номер патента: 1828166
Автор: Гельфенбейн
Формула
1. Роторная машина, содержащая ротор на упругих опорах с промежуточными массами и корпус, отличающаяся тем, что, с целью снижения уровня ее вибраций и снижения чувствительности корпуса к разбалансировке роторов при выполнении промежуточной массы в виде второго ротора, опоры роторов выполнены с различными жесткостями, опеределяемыми из следующих выражений
C1= m1 ![]() 22ном-m2
22ном-m2 ![]() 21ном
21ном
C2= m2 ![]() 21ном,
21ном,
где C1 жесткость опоры 1-го ротора,
C2 жесткость опоры 2 го ротора, расположенной на 1-ом роторе,
m1, m2 массы 1-го и 2 го роторов, приведенные к плоскостям опор,![]() 1ном,
1ном, ![]() 2ном номинальные круговые частоты вращения 1-го и 2 го роторов.
2ном номинальные круговые частоты вращения 1-го и 2 го роторов.
2. Роторная машина, содержащая ротор на упругих опорах с промежуточными массами и корпус, отличающаяся тем, что с целью снижения уровня ее вибрации и снижения чувствительности корпуса к разбалансировке роторов при выполнении промежуточной массы в виде второго ротора, при изменении круговых частот вращения роторов в диапазоне ![]() 1мин-
1мин- ![]() 1макс и
1макс и ![]() 2мин-
2мин- ![]() 2макс опоры роторов выполнены с различными жесткостями, определяемыми из следующих выражений:
2макс опоры роторов выполнены с различными жесткостями, определяемыми из следующих выражений:
C1= m1(K1 ![]() 22макс)2-m2
22макс)2-m2 ![]() 21ном
21ном
C2= m2(K2 ![]() 1мин)2,
1мин)2,
где C1, C2 жесткости опор 1 и 2 роторов;![]() 1мин,
1мин, ![]() 1макс соответственно минимальная и максимальная круговая частота вращения 1-го ротора;
1макс соответственно минимальная и максимальная круговая частота вращения 1-го ротора;![]() 2мин,
2мин, ![]() 2макс минимальная и максимальная частота 1-го ротора;
2макс минимальная и максимальная частота 1-го ротора;
m1, M2 массы 1-го и 2-го роторов, приведенные к плоскостям опор,
К1, К2 настроечные коэффициенты, равные 1,0 1,1 и 0,9 - 1,0 соответственно.
Описание
Целью изобретения является повышение эффективности взаимного гашения колебаний системы соосных роторов и снижение чувствительности этой системы к разбалансировке роторов путем использования принципа настройки динамического гасителя колебаний за счет соответствующего выбора жесткостей С1 и С2 опор двух соосных роторов.
Сущность изобретения сводится к выполнению опор с жесткостями, значения которых получаются в результате расчета системы двух соосных роторов, настроенных на режим взаимного динамического гашения колебаний.
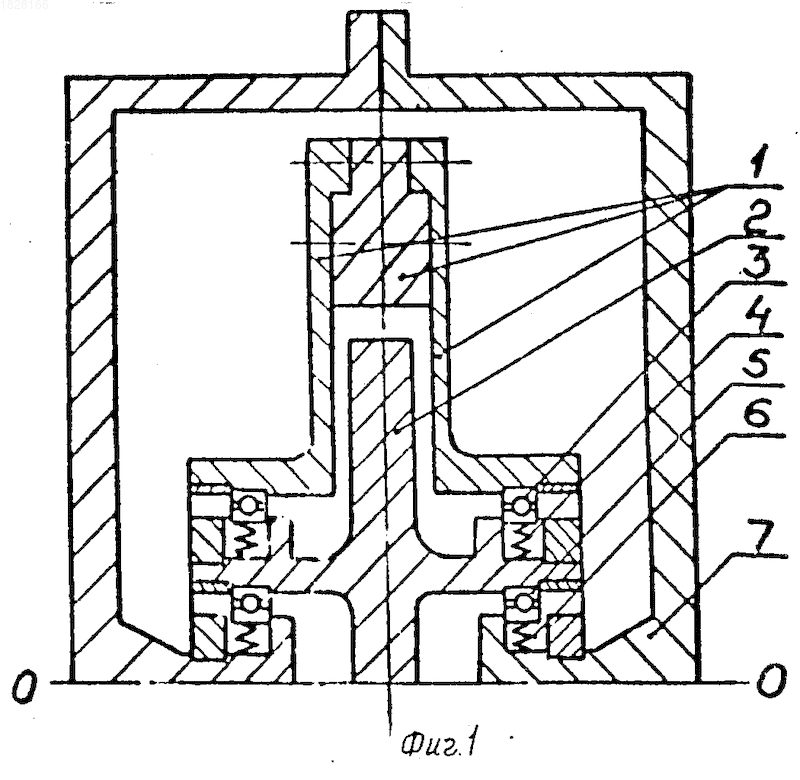
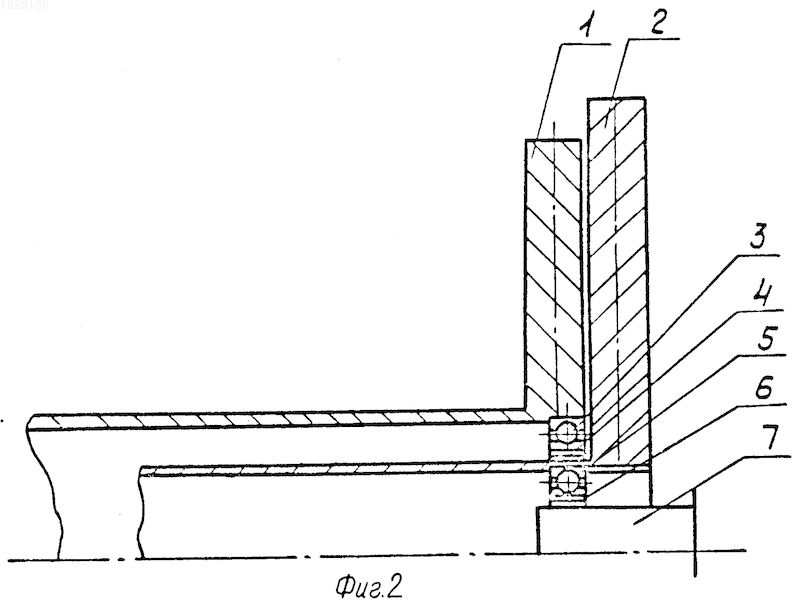
На фиг. 1 изображена схема двух симметричных соосных роторов; на фиг.2 схема части двух асимметричных роторов.
Ротор 1 опирается на ротор 2, через промежуточный подшипник 3, установленный через упругие элементы 4, ротор 2 через подшипник 5 и упругие элементы 6 опираются на корпус 7. Задача сводит к обеспечению определенных жесткостей опор за счет упругих элементов 4 и 6.
Для пояснения физической сущности взаимного гашения колебаний двух соосных роторов приведем аналитическое решение данной задачи. Для придания наглядности и упрощения аналитических выводов будем рассматривать симметричную систему фиг.1 с жесткими роторами.
В симметричной системе гашение колебаний происходит в каждой опоре статора, в асимметричной системе (фиг.2), в которой массы сосредоточены в плоскостях одной из опор каждого ротора, гашение колебаний происходит именно в этих плоскостях, которые в большинстве конструкций авиационных ГТД совпадают между собою.
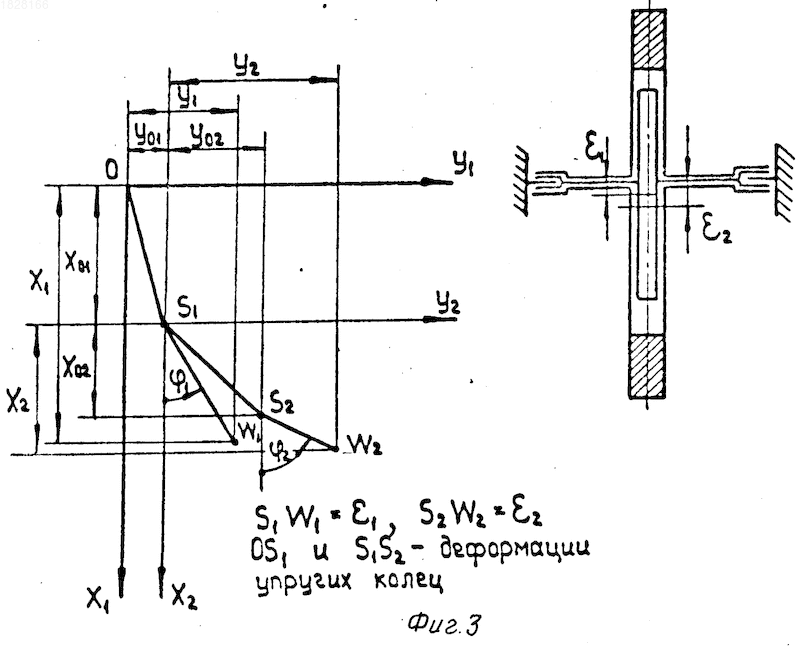
На фиг.3 представлена схема двух соосных однодисковых роторов, массы которых сосредоточены в дисках, а движение определяется движением цапфы в любой из плоскостей опор. Движение будем рассматривать в неподвижной системе координат Х, Y, начало которой совместим с центром диска ротора 1 при отсутствии деформации упругих элементов его корпуса. Уравнение кинематической энергии Т центров масс роторов и потенциальной энергии П упругих элементов роторной системы имеют вид
T
П
где m1 и m2 массы дисков роторов I и II;
Х1, Y1 и Х2, Y2 координаты центров масс дисков I и II;
Х01, Y01 и Х02, Y02 координаты центров дисков I и II;
I1, I2 и М1, М2 моменты инерции дисков I, II и внешние крутящие моменты на валах I, II соответственно;
С1 и С2 жесткости упругих элементов.
Используя функцию Лангранже L Т-П, получим следующие уравнения движения:
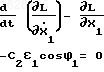
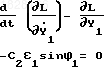
Считая частоты вращения валов постоянными, т.к.
m
m
(2)
Частное решение этих уравнений представим в виде сумм
Z*01=A1 ei
Z*02=A2 ei
(3)
Амплитуды А1, А2 определяются при
Рассмотрим первый из этих случаев, для чего подставим в (2) значения:
Z01= A1e
Z02= A2e
В результате получим:
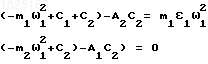
(4)
Уравнения (2) и решения (3) при
обобщенные координаты Z*01 и Z*02 являются комплексными величинами, т.е. рассматриваемая система имеет 4 степени свободы, а не две, как в гасителе Фрама;
движение каждой из масс m1 и m2 происходит в плоскости, а не вдоль линии;
каждая из масс подвержена двум соответствующим возбуждениям с частотами
Подставим в уравнения (4) следующие обозначения: F01= m1
В результате получим
A1=
A2=
(5)
Условие настройки, обеспечивающее нулевое значение амплитуды А1, имеет вид
1-
(6)
Малые амплитуды А2 колебания массы m2, при соблюдении настройки (6), обеспечиваются малым эксцентриситетом
Рассмотрим второй случай
Z01= B1e
Z02= B2e
Получим
В1(-m1
B2(-m2
Обозначим F02 m2
B1=
B2=
(8) где
Настройка системы, при которой В2 0, определяется условием
1+
С1
При этом B1=
Подставив (5) и (8) в (3), получим частное решение:
Z*01=
Z*02=
(10)
Уравнения (10) позволяют оптимизировать и определить численно перемещения Z*01 и Z*02 каждого из роторов в любом диапазоне изменения частот вращения
При выполнении настроек (6( и (9) решение (10) упрощается и приобретает вид:
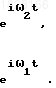
(11)
Из полученного результата видно, что амплитуда перемещения ротора II пропорциональна дисбалансу ротора I и наоборот. Кроме того, чем выше жесткость C2 соединения промежуточного подшипника с роторами, тем меньшем амплитуда перемещения каждого ротора.
На фиг. 1 и 2 обозначены: 1 ротор II, опираемый на ротор I; 2 ротор I, опираемый на статор; 3 промежуточный подшипник; 4 упругий элемент, установленный под промежуточный подшипник на роторе I; 5 подшипник ротора I; 6 упругий элемент, установленный под подшипник ротора I на статоре; 7 статор.
В качестве примера конкретного выполнения рассмотрим роторную систему, приведенную на фиг.1, при следующих параметрах:
m1 0,05 кг
m2 0,09 кг
Задача состоит в определении величин жесткостей С1 и С2 упругих элементов, при которых амплитуды колебаний роторов остаются весьма малыми во всем диапазоне изменения частот вращения роторов I, II.
Рассмотрим два варианта настройки роторной системы.
Вариант 1 Настроим роторную систему на номинальные частоты вращения, для чего определим жесткости опор согласно (6) и (9).
С1 m1
0,017
Определим постоянные величины
P21
P22
Согласно (5) и (7) определим:
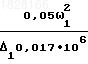 2,94
2,94 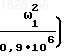 ;
;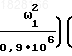 5,76-
5,76- 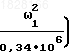 4,76;
4,76;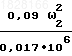 5,5
5,5 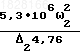
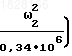 ;
;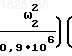 5,76-
5,76- 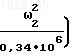 4,76.
4,76.Задаваясь значениями
Для определения амплитуд А1, А2, В1 и В2 необходимо значение величин
При такой сбалансированности роторов максимальная из амплитуд В1 не превышает 0,025 мм.
Если допустить повышенный уровень разбалансировки роторов, при котором
А1 0,2
А2 0,6
В1 6,1
В2 1,9
Отметим здесь повышенный уровень амплитуд В1 и В2 и их резонансный характер роста на максимальных частотах вращения ротора II.
Амплитуды эти могут быть уменьшены использованием иных вариантов настройки, один из которых рассмотрен ниже.
Вариант II. Настроим систему на режим
Подставим эти значения в выражения
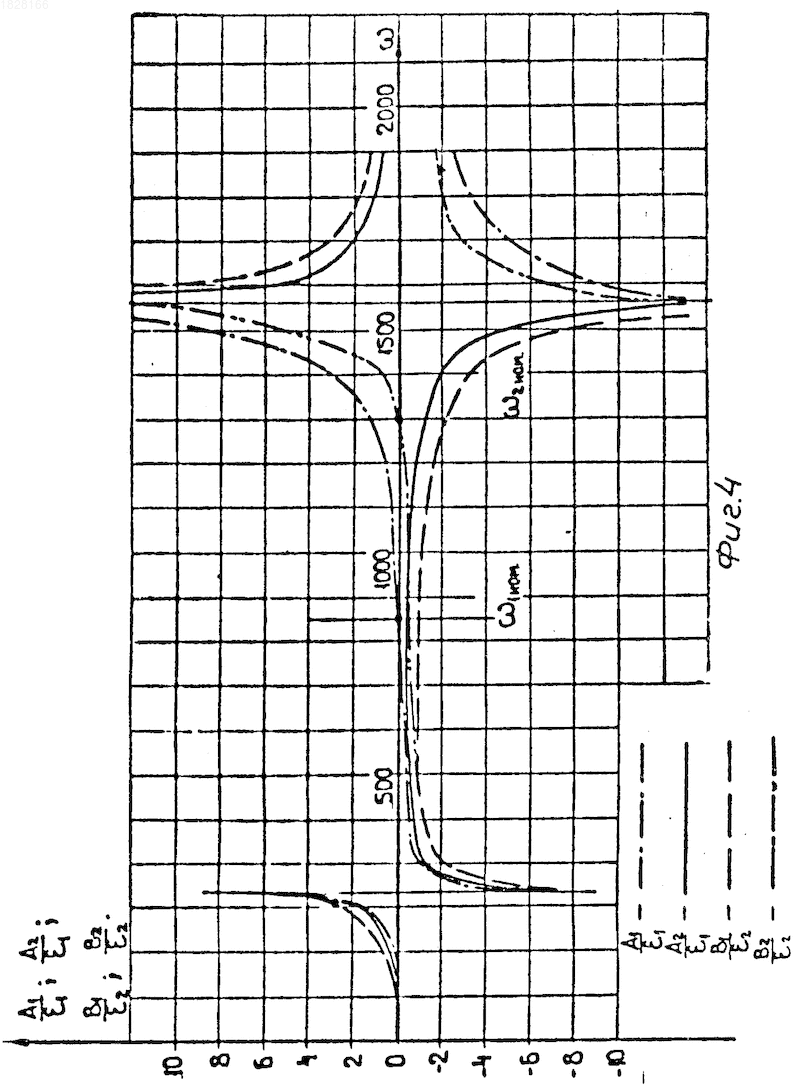
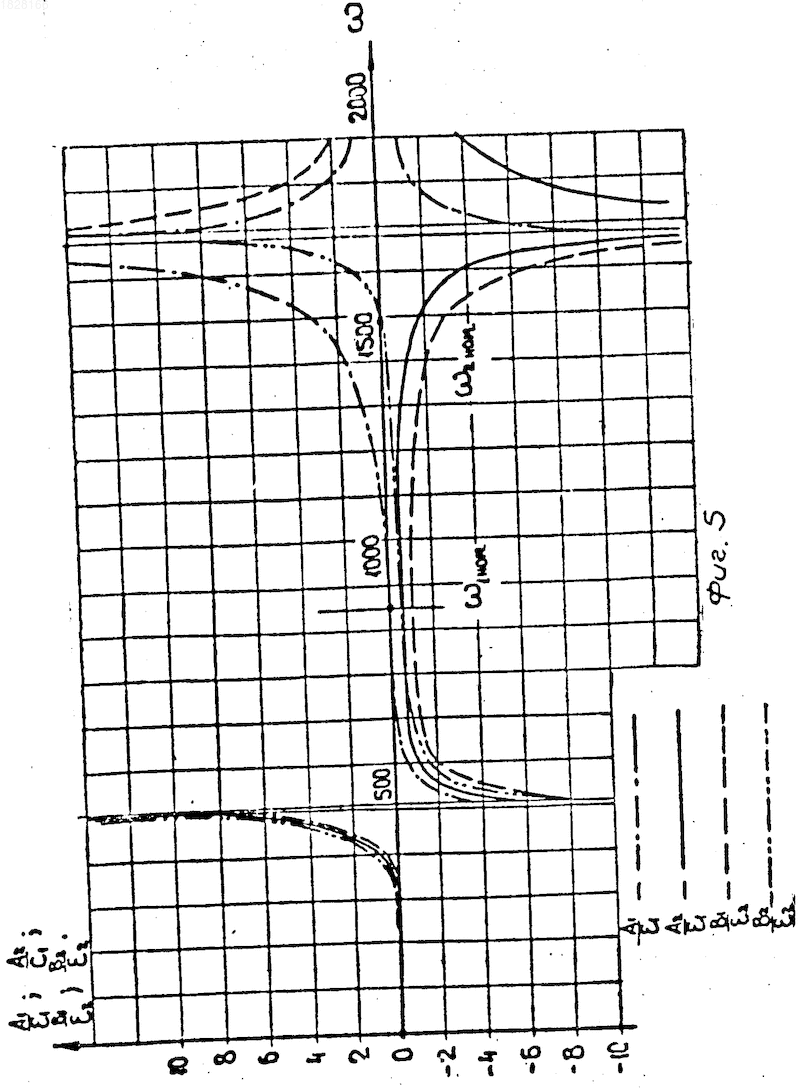
На фиг.5 приведен расчет при жесткости С2 по варианту 1, а жесткость C1=
Резонансные частоты определяются из условия 1 0 и
P201= P202= P20
Так как Р2 0,9
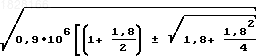
что составляет 510 и 1790 1/c.
Таким образом, при этой настройке обеспечивается достаточный запас по отношению к резонансным частотам системы, что достигается выбором настроечных частот вращения роторов по результатам расчетов и анализов нескольких вариантов.
Следовательно, с целью обеспечения большего удаления максимальных и минимальных частот вращения каждого ротора от резонансов системы, частоты настройки роторов могут отличаться от номинальных частот вращения роторов на
Этим примером показана возможность настройки системы соосных, упруго связанных роторов на взаимное гашение колебаний их масс. Из анализа решения (фиг. 4,5) видно, что настройка состоит в расположении рабочего диапазона частот вращения роторов (
Обеспечение заданной жесткости опор реализуется с допусками. Если назначать допуски с учетом возможного расширения настроечного диапазона частот вращения, а именно от (0,9 1,0)
C1 m1(K1
С2 m2(K2
Настройка роторной системы на взаимное гашение колебаний обеспечивает низкий уровень вибраций машин, что в свою очередь определяет ряд технико-экономических показателей всей машины, таких как: надежность, повышенный ресурс, малая утомляемость экипажа в случае двигателей транспортных машин, точность работы показаний установленной на машине аппаратуры, стабильный уровень основных параметров машины и т.п.
Кроме того, применительно к роторам авиационных двигателей малая амплитуда колебаний роторов позволяет уменьшить величины радиальных зазоров между элементами роторов и статора, что является определяющим фактором в получении высоких удельных газодинамических параметров ГТД в целом.
Использование: при изготовлении роторных машин, включающих в себя два соосных ротора, из которых I-й упруго опирается на корпус, а II-ой ротор упруго опирается на I-й ротор. Такие роторные системы часто используются в авиационных газотурбинных двигателях. Сущность изобретения сводится к выполнению опор с жесткостями, которые обеспечивают движение ротора с взаимным гашением их колебаний. Значение жесткостей опор заданы аналитически, как функция приведенных масс роторов и их круговых частот вращения. 2 с.п. ф-лы, 5 ил.
Рисунки
Заявка
4791719/06, 09.11.1989
Ленинградское научно-производственное объединение им. В. Я. Климова
Гельфенбейн Л. С
МПК / Метки
МПК: F01D 5/10
Опубликовано: 10.09.1995
Код ссылки
<a href="https://patents.su/0-1828166-rotornaya-mashina-ee-varianty.html" target="_blank" rel="follow" title="База патентов СССР">Роторная машина (ее варианты)</a>
Предыдущий патент: Способ дробления материала в конусной дробилке и конусная дробилка
Следующий патент: Стенд для обкатки и контроля двигателя внутреннего сгорания
Случайный патент: Противоскользящий цилиндр