Способ определения весовой функции физической системы с переменными параметрами

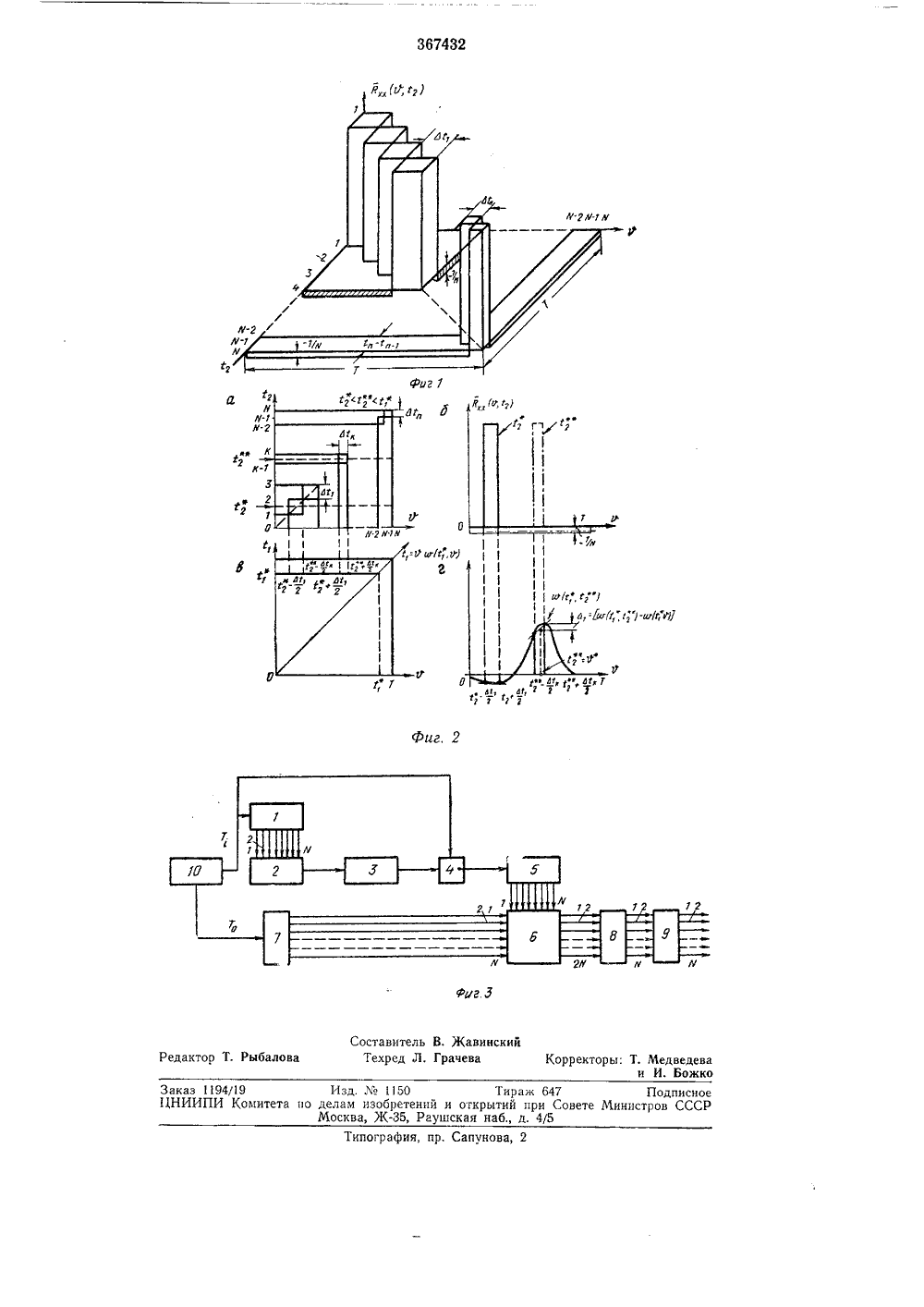
367432 ОПИСАНИЕ ИЗОБРЕТЕНИЯ К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ Союз Советских Социалистических РеспубликЗависимое от авт. свидетельстваЗаявлено 15 Л 1,1971 (ЭЬ 1626379/18-24)с присоединением заявкиКл. 6 06 д 752 иоритет Комитет ло делам иаобретений и открытий лри Совете Министров СССРК 681,333:519.2 (088.8) публиковано 33 х 1,1973, Бюллетень8 ата опубликования описания 27.17.1973 Авторизобретеии В, ф, Авраменко аявител ПОСОБ ОПРЕДЕЛЕНИЯ ВЕСОВОЙ ФУНКЦИИ ФИЗИЧЕСК СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ2 Способ относится к области применения средств вычислительной техники для анализа систем управления статистическими методами.Изобретение представляет собой способ определения весовой функции одного класса систем управления с переменными параметрами, к которому относятся, например, системы управления конечным состоянием, а также системы управления летательными объектами.Известные способы определения весовой функции системы с переменными параметрами основаны на множественном корреляционном анализе реакции системы на входные случайные и двоичные псевдослучайные сигналы.Однако при осуществлении этих способов выполняют довольно большой объем экспериментальных и вычислительных работ.Анализ ошибок измерения, наиболее близкого к предлагаемому способу, показал, что возможно уменьшение объема работ за счет более равномерного распределения точности измерения по определенному сечению весовой функции системы.По предложенному способу, с целью сокращения времени определения весовой функции на участках рабочего интервала системы управления с шагом, равным текущей длительности такта, производят дискретные выборки значений выходных сигналов системы, возникающих от двоичных псевдослучайных сигналов, имеющих переменную длительность так та, которую скачкообразно изменяют при переходе с одного участка на другой. По общей совокупности выборок, взятых для каждого участка измерения с весом, обратно пропорциональным длительности его такта, вычисля ют множественную функцию взаимной корреляции. Введение переменнои длительности тактапозволяет более экономично определять искомое сечение весовой функции. При этом в не которых случаях для сечений весовой функции, предшествующих искомому, могут быть получены либо сравнительно невысокая точность измерений, либо заведомо меньшее число значений весовой функции, чем это необ- О ходимо. Однако для рассматриваемого класса систем наиболее существенны динамические и случайные ошибки в момент окончания управления, для вычисления которых используют единственное сечение весовой функции, 5 взятое для этого момента времени, Полученного объема информации о весовой функции вполне достаточно для аналитической оценки точности исследуемых систем, тем самым доказывается практическая целесообразность О использования предлагаемого способа.3На фиг. 1 приведено пространственное изображение нормированной множественной автокорреляционной функции Рхх (о, Ь) двоичных псевдослучайных сигналов Хл (1), Х(1),Х (1) со скачкообразно изменяющейся в фиксированные на интервале О, Т) моменты времени 1, (=1, 2, , и) длительностью тактового интервала Л 1 на фиг. 2, а, б, в, г, дан график, иллюстрирующий способ (а - проекция 1 Ьх (о, 1) на плоскость ооЬ, б - два сечения Рхх (о, 1) плоскостями, перпендикулярными оси о 1 и проходящими через точки 1, и 1,"; в - графическое изображение области существования весовой функции лл (1 ь о) и ее разыскиваемого сечения при 1 л=1 г - процесс определения значения сопряженной весовой функции в (1 о), основанный на использовании теоремы о среднем; на фиг, 3 показан упрощенный пример блок-схемы для осуществления предложенного способа.Схема содержит генератор 1 псевдослучайных сигналов, синхронизируемый импульсами переменного периода Т (1;), коммутатор 2, осуществляющий последовательное подключение (безразлично в каком порядке) сформированных сигналов к входу исследуемой системы в начале ее рабочего цикла, исследуемую систему 3 с переменными параметрами; ключ 4, снимающий выходные сигналы системы с переменной дискретностью, коммутатор б, распределяющий снятые ключом 4 дискретные значения -го выходного сигнала по У каналам, коммутатор б, осуществляющий в зависимости от знака двоичных сигналов, снимаемых с генератора 7, коммутацию поступающей на его вход информации по 2 У каналов, блок 8 усилителей и инверторов с коэффициентами усиления, зависящими от номера канала, блок 9 сумматоров, суммирующих и запоминающих поступающую на них дискретную информацию на временном интервале 11 Т, блок 10 программного механизма, осуществляющего в заданные моменты времени скачкообразное изменение периода Т(1;) синхронизирующих импульсов по заданному закону.Предложенный способ состоит в следующем.Пусть имеется одномерная система автоматического управления с переменными параметрами, работающая при неизменных начальных условиях на конечном интервале времени О, Т 1. Для определения ее сопряженной весовой функции разобьем вес в рабочий интервал О, Т 1 на и участков таким образом, чтобы имела место следующая система неравенства:О = 1, (; ( +л ( 1= Т. (1)При этом дополнительно потребуется, чтобы каждый из 0=2 - 1 двоичных псевдослучайных сигналов Х, (1), Х (1) Х (1) из периодического двоичного псевдослучайного сигнала Хаффмана Хо (1), период измене 4ния которого равен рабочему циклу системы, путем всевозможных сдвигов на целое число тактов, имел при переходе от одного участка к другому скачкообразно изменяющуюся по 5 определенному закону длительность тактовогоинтервала, Если через Мл обозначить длительность тактового интервала сигнала Х (1) (1=1, 2, , У) на участке (1; л - 1;), то при этом на интервале О, Т 1 должно выполнять ся условие(2) 15 Тогда, подавая в каждый Й-й рабочий циклисследуемой системы А-й псевдослучайный двоичный сигнал Х (1) с изменяющейся длительностью тактового интервала, и регистрируя реакции системы У (1) на эти сигналы, 20 вычислим множественную функцию взаимнойкорреляции(о) 40- множественная автокорреляционная функция сигналов , , Х, (1), , Х(1);о - момент подачи возмущения на систему;6 - момент измерения (наблюдения), принадлежащий интервалу времени О, Т. 50 Для физически реализуемых систем независимые переменные уравнения (4) связаны условием 1(1 л(Т. При этом диапазоны изменения переменных 1 ь 1 и о совпадают и ограничиваются величиной интервала О, Т.55 Вычисление множественной функции взаимной корреляции по формуле (3) с целью определения весовой функции исследуемой системы эквивалентно решению интегрального уравнения (4). При этом точность вычисле ний и объем экспериментальных работ существенно зависит от корреляционных свойств задаваемых на систему сигналов.Известно, что для псевдослучайных сигналов с малой длительностью Л 1 и большим чис лом А=2 - 1 множественная автокорреляДля линейных систем управления с переменными параметрами, имеющих нулевые начальные условия, связь между множественной функцией взаимной корреляции и весовой 30 функцией системы определяют обобщенныминтегральным уравнением Винера-Ли1,гх ( з) = ф( ) Их(" ) 1 п (4)о35 где в (1,о) - весовая функция системы с переменными параметрами;(6) Мсг где а - амплитуда входного сигнала. 5ционная функция с точностью до постоянного множителя совпадает с весовой функцией исследуемой системы.Однако при этом объем экспериментальных и вычислительных работ определяется тем же числом Л=2" - 1, которое является достаточно большим.Для сокращения объема работ задачу решают с использованием двоичных сигналов с малым числом М и переменной длительностью такта.Пользуясь обычным методом систематической обработки реализации нестационарного случайного процесса, задаваемого на интервале О, Т, вычислим множественную авто- корреляционную функцию двоичных псевдослучайных сигналов Хс (с), Х 2 (1), , Хс (с) и ее графическое построение в координатах оо 12. В результате получим пространственную фигуру, изображенную на фиг. 1.На фиг. 1 показана нормированная множественная автокорреляционная функция Йхх(п, 12), а на фиг. 2 - ее сечение плоско- СТЬЮ ООГ 2.В связи с тем, что множественная автокорреляционная функция входных сигналов Рхх (1), 62) представляет собой последовательность пар аллепипедов, группирующихся вдоль прямой о = 12, основаниями которых служат квадраты со сторонами, равными Мс=1, 2, 3 и), правая часть уравнения (4) для всех 12(11 и фиксированных значений 1)=1 принадлежащих интервалу О, Т, приводится на участке (11 - 11-1) к такому виду)с2йР )=" Р ИвУьссс, -2 3674326которая существенно зависит от длительноститактового интервала М;.Второе слагаемое в правой части равенства(У+1) Ы,о- систематическая ошибка измерения способа, возникающая из-за наличия отрицательной составляющей множественной автокорреляционной функции входных сигналов,Влияние Л 2 (1,) проявляется в том, что припостроении графика сопряженной весовой функции, полученного в результате обработки экспериментальных данных, наблюдается его смещение по оси абсцисс. Величина этого смещения для конкретно выбранного момента времени 1)=1, постоянна и зависит только от 25 характера изменения сопряженной весовойфункции.Учитывая изложенное, для всех 12(1 находящихся на участке (11 - 11интервала О, Т 1, окончательно получим30Ргх(11, ) а М, ХХ 11) Йг) + Л (1 г) + Лг Р 1)1 (9)55 Таким образом, подавая на вход системы спеременными параметрами, работающей из цикла в цикл при неизменных (в данном случае нулевых) начальных условиях, всевозможные циклически сдвинутые друг относи тельно друга на целое число тактов двоичныепсевдослучайные сигналы, имеющие на участках (1, - 1,- (1= 1, 2 и) длительность тактового интервала Л 1;, и определяя по результатам эксперимента для этих участков 45 множественную функцию взаимной корреляции (3), получим с точностью до известногоЛ)+1нам множителя а 2 Л 1; и ошибок Л, (112)Преобразование уравнения (4) к виду (6) наглядно иллюстрируется с помощью графических построений, отображенных на фиг. 2, а, б, в и г. Однако при использовании этих графических построений для вывода уравнения (6) необходимо учитывать, что применяемая в них множественная автокорреляционная функция входных сигналов является нормированной, в то время как в уравнении (4) корреляционные функции не нормированы.Анализ первого слагаемого равенства (6) позволяет установить величину динамической ошибки измеренийДс Р 1 г) = Г 2) (1, Р) - 1 СС(11 1 г) (7) 50 и Л. (1,) сопряженную весовую функцию исследуемой системы для любого момента времени 1) =11, принадлежащего интервалу О, Т).У+1Так как величина множителя а 2 М, су 55щественно зависит от длительности такта Л 1;, то в связи с тем, что она является переменной, при переходе с одного участка измерения интервала О, Т)1 на другой наблюдается из менение масштаба, Это может создать дополнительные трудности при графических построениях результатов обработки. Для устране.ния этого эффекта необходимо осуществлять одновременно с изменением величины такто вого интервала изменени я 8 лп 8 ты входно.(11) :с, 12 7го сигнала таким образом, чтобы для любойпары участков интервала 10, Т 1 имело месторавенство аИ, = Ьа М = сопят ро) или принимать меры для аппаратурной компенсации изменения масштаба измерений. Применение аппаратурной компенсации из-за ее простоты имеет существенные преимущества перед сигнальной компенсацией, связанной с выполнением условий (10). Поэтому в дальнейшем будем исходить из предположения, что используется именно аппаратурная компенсация.Определим, каким условиям должны удовлетворять параметры входных сигналов, выполнение которых обеспечивает наименьший объем экспериментальных и вычислительных работ при заданных требованиях на точность измерений,Динамическая ошибка способа в форме (7) приводится к видудфоп (1 р)Р 1 г) -Отсюда следует, что составляющие динамической ошибки измерения по положению и по скорости отсутствуют, а наибольшее влияние на точность измерений оказывают составляющие ошибки по ускорению и более высоким производным.Систематическая ошибка способа Л ( ) для заданного сечения весовой функции системы является величиной постоянной и легко устранимой при построении графика сопряженной весовой функции. Поэтому в дальнейшем ее влияние на точность измерений не учитывается,Анализ ошибок способа позволяет утверждать, что наименьшее влияние на точность измерений оказывают составляющие динамической ошибки, находящиеся в прямой зависимости от величины второй и более высоких частных производных весовой функции ж (1 о) по аргументу о, и что единственным способом ее уменьшения является сокращение длины тактового интервала М,. Однако распределение величины второй и более высоких производных по сечению весовой функции не является равномерным. Если величина тактового интервала Ы; выбрана из условия обеспечения приемлемой точности измерения и остается постоянной на интервале О, Т), это приводит к тому, что на участках интервала 10, Т 1, где абсолютные значения величин второй и более высоких производных от весовой функции наибольшие, точность измерений соответствует заданной, а на других значительно превышает ее, в чем нет особой необходимости.Использование постоянной ЛА на интервале 10, Т влечет за собой необоснованное увели 10 15 20 25 зо З 5 40 45 5 О 55 60 65 8чение объема У экспериментальных и вычислительных работ, величина которого получается путем округления числа И =ТМ до ближайшего большого числа, равного 2" - 1.Если соблюдать дополнительное условие1 -для каждого искомого сечения весовой функции в (1 ь о), то можно всегда определить закон изменения во времени длины тактового интервала, в соответствии с которым определяются параметры входных псевдослучайных сигналов, и достигается более равномерное распределение точности измерения и меньший объем эксперимента,чьных и вычислительных работ.Однако при осуществлении предложенного способа возникает ряд трудностей, несколько снижающих его эффективность. К ним относится, например, отсутствие точной информации о характере весовой функции и ее частных производных, на основании которой может быть получен закон изменения во времени длины тактового интервала. Но в этом нет особой необходимости; на основании самой общей информации о характеое изменения сопряженной весовой функции на измеряемом интервале 0, Тч, полученной, например, либо в процессе предварительных более грубых измерений, либо в результате анализа косвенных характеристик динамики исследуемой системы, весь интервал 0, Т 1 может быть трубо разбит на ряд участков (1; - 1;-) (= =1, 2, , и), в пределах каждого из которых М, неизменна, но при переходе от одного к другому изменяется скачком. На тех участках, где наблюдается сравнительно медленное изменение значений весовой функции, длина тактового интервала М; может быть выбрана сравнительно большой, при быстром - малой.Несмотря на то, что изложенное выше относится к системам управления, работаюгцим из цикла в цикл при неизменных нулевых начальных условиях, полученные результаты справедливы и для ненулевых начальных условий. Наличие ненулевых начальны. условий приводит к изменению величины систематической ошибки способа. Упрощенный пример его экспериментально-вычислительной блоксхемы приведен на фиг. 3.Блок 10 представляет собой программный механизм, скачкообразно изменяющий в заданные моменты времени 1; (1=1, 2, , и) частоту синхронизируюших 1 генератор 1 и ключ 4) импульсов по заданному закону. Конструктивно он может быть выпо,чнен в виде коммутатора, поочередно подключающего генераторы импульсов с фиксированными частотами в различные моменты времени, либо в виде генератора с управляемой частотой. Управление генератором осуществляется напряжением, которое претерпевает скачкообразное изменение амплитуды в дискретные моменты времени. Кроме того, блок 10 содер,/-ш/АЖИ И,2 Г 2иг,Составитель В. Жавинскнй актор Т. Рыбалова Техред Л. Грачева Корректоры: Т, Медведеваи И, Божко Заказ 1194/19 Изд. ЛЪ 1150 Тираж 647 Подписно ЦНИИПИ Комитета по делам изобретений и открытий при Совете Министров ССС Москва, Ж, Раушская наб., д. 4/5ипография, пр, Сапунов