Устройство для вычисления булевых функций

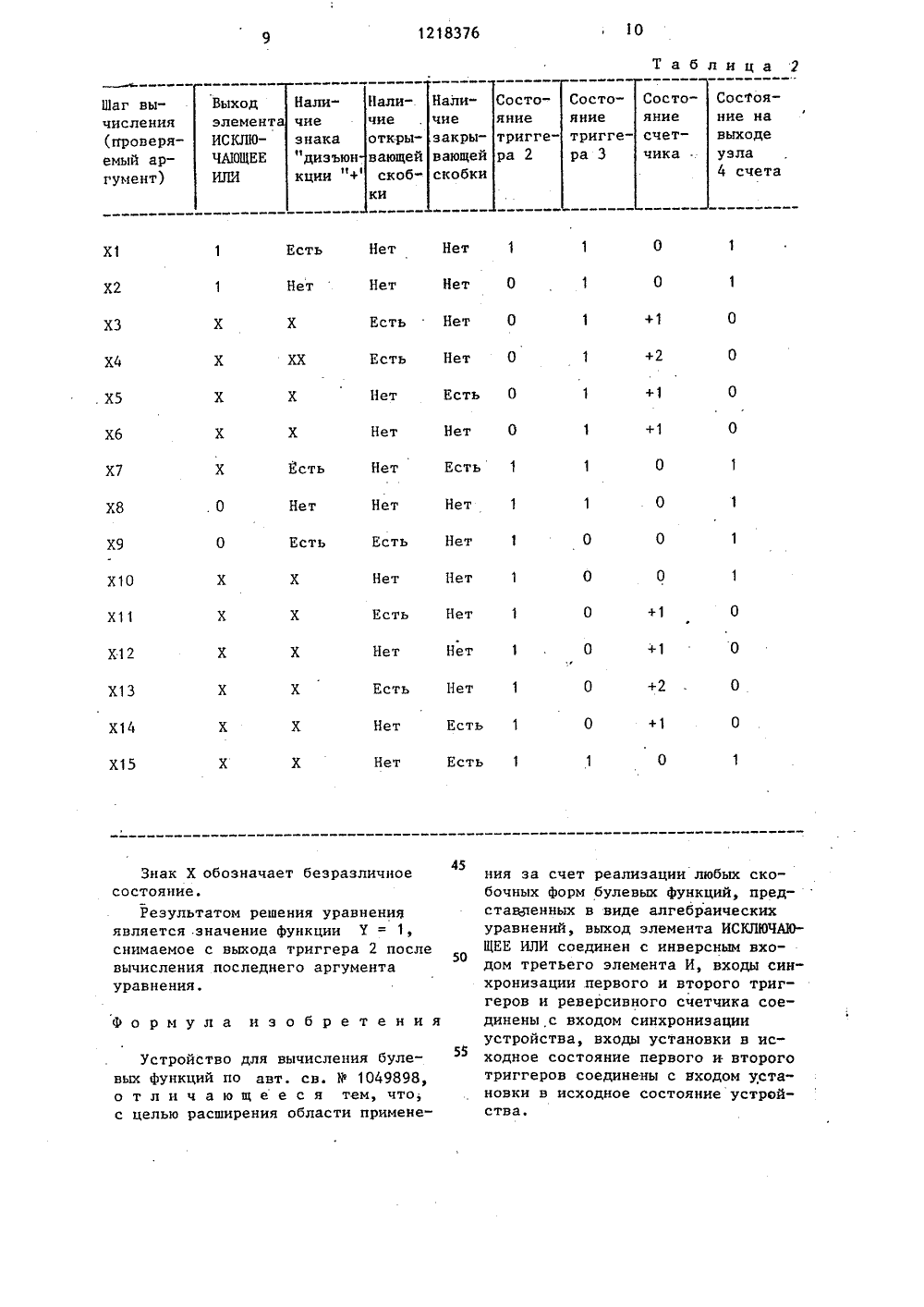
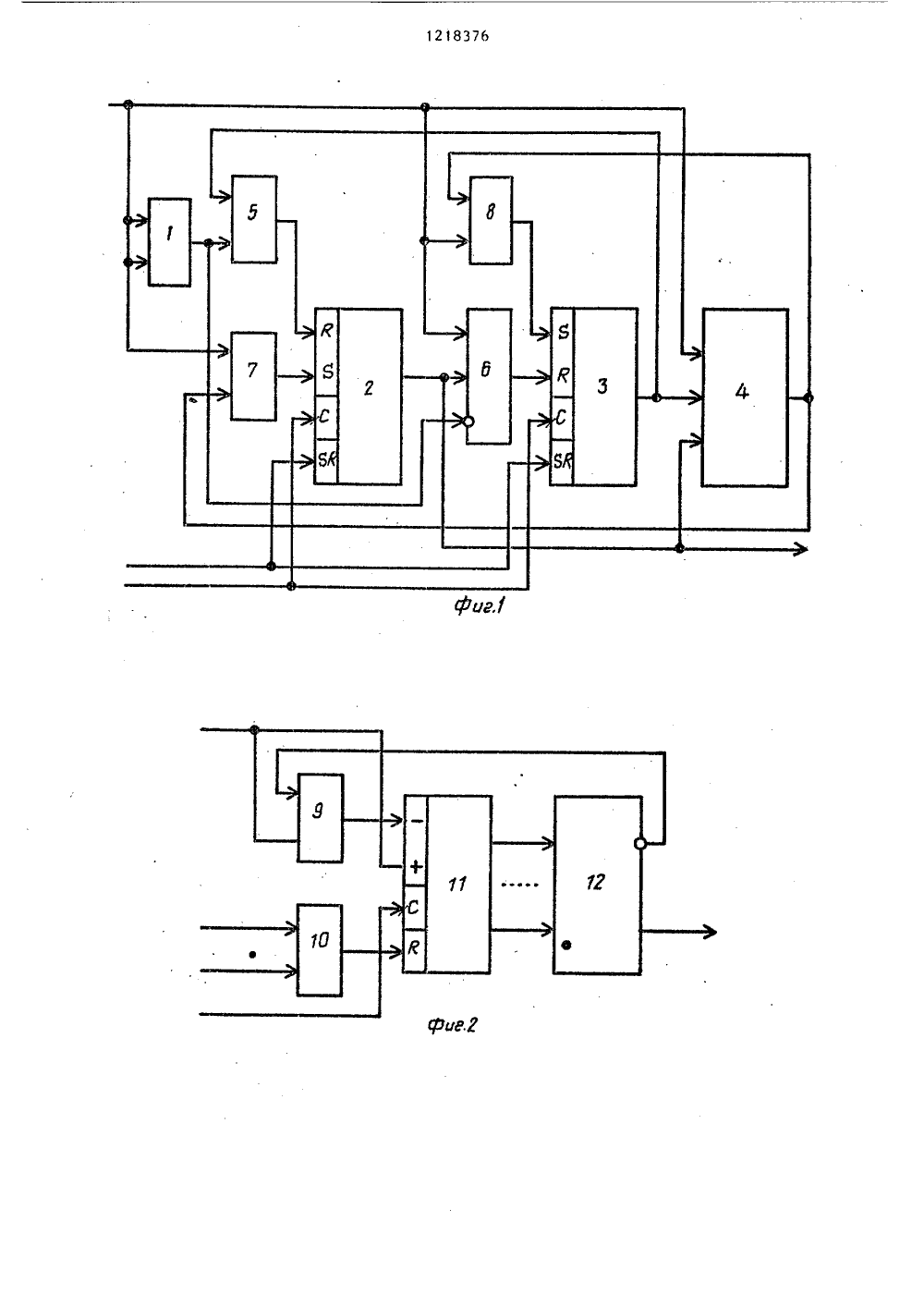
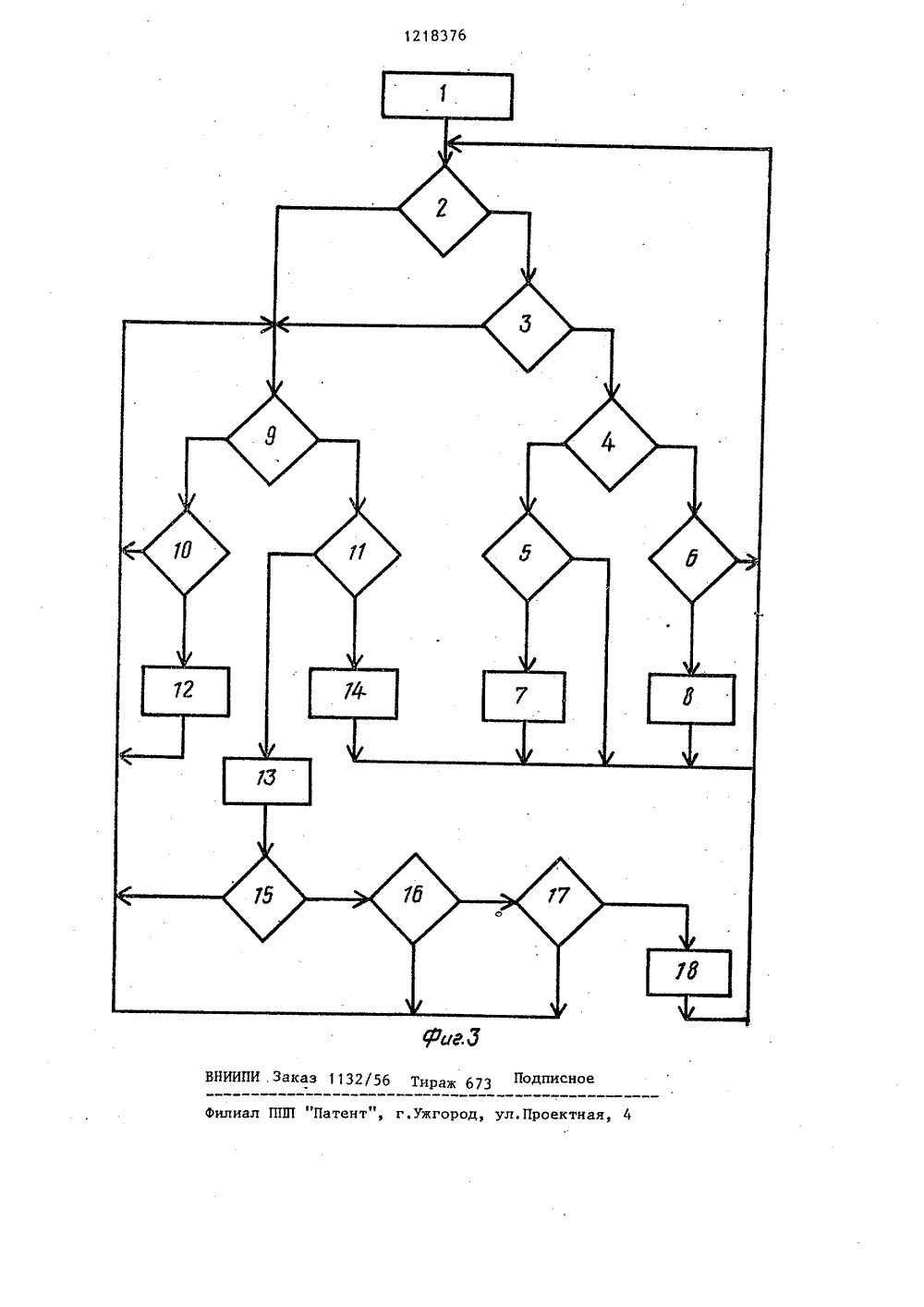
СОЮЗ СОЙЕТСНИХСОЦИАЛИСТИЧЕСНИХРЕСПУБЛИН 9) (11),ш 4 С 06 Р 7/О ПИСАНИЕ ИЗОБРЕТЕНИ 00 СЬ ГОСУДАРСТВЕННЫЙ НОМИТЕТ СССР ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТНРЫТИ ТОРСНОМУ СВИДЕТЕЛЬСТВ(56) Авторское свидетельство СССР.В 1049898, кл. С 06 Г 7/00, 1982,(54) УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ(57) Изобретение относится к автома тике и вычислительной технике и может быть использовано в программируемых системах управления технологическими объектами алгоритм управления которых описывается с помощью булевых функций, в частности в программируемых контроллерах и управляющих вычислительных машинах. Цель изобретения - расширение области применения устройства за счет реализации любых скобочных форм булевых функций, представленных в виде алгебраических уравнений. Устройство содержит элементы И, элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, первый и второй триггеры, узел счета скобок. В процессе вычисления на информационный вход подаются действительные значения аргументов, на управляющие входы - сигналы "Значение аргумента, указанное в уравнении", "Дизъюнкция", "Закрывающая скобка", "Открывающая скобка". Эти сигналы р подаются в том порядке, в котороме соответствующие им символы записаны в уравнении, После вычисления последнего аргумента уравнения значе- С ние функции снимается с выхода пер 1 ного триггера. Изобретение дополни" С: тельное к авт.св. У 1049898. 3 ил, 2 табл.ЭЯпроверить состояние счетчика 11 наравенство нулю; блок 12 - инкрементировать содержимое счетчика 11; блок13 - декрементировать содержимоесчетчика 11 блок 14 - установитьтриггер 3 в единичное состояние,блок 15 - проверить состояние тригГера 2 на равенство нулю, блок 16 -проверить состояние счетчика 11 на1 О равенство нулю, блок 17 - проверитьналичие знака дизъюнкции "+"," блок18 - установить триггер 2 в единичное состояние.Устройство использует для вычисле.1 Б ния булевых функций алгебраическихуравнений знак дизъюнкции+ , открывающие и закрывающие скобки, чтодает возможность реализовать скобочпые Формы булевых функций, представ 20 ленные в виде алгебраических уравнений. При этом отпадает необходимость в разработке принципиальныхэлектрических схем за счет того,что программирование производитсянепосредственно по уравнению, а непо электрической схеме. 11 аксимальнооблегчается труд программиста,так как любое уравнение являетсяи программой его решения, поэтомудля программирования достаточнопросто переписать это уравнениев память устройства без каких-либопреобразований, Кроме того, программирование по уравнению:позволяет автоматизировать ввод программы35(например вводить программу от вычислительной машины),Решить булевое уравнение -значит найти его значение на данномнаборе аргументов. Для любого булевого уравнения вычисления ведут в порядке естественной записи аргументов,т.е. слева направо.Пример уравнения:45 Х 1 " (Х 2 + ХЗ + Х 4) (Х 5 + Хбфх(Х 7 + Х 8 к Х 9 + Х 10 = У (1)Индексы при аргументах определяют порядок вычисления,В начале вычисления устанавливают значение функции, равное 1. Решаютуравнение, вычисляя последовательноаргументы в следующем порядке. Обозначают единицей значение аргумента,указанное в уравнении, если этотаргумент записан для знакаинверсии(аргументы Х 1, Х 3, Х 4, Х 5, Х 7, Х 8,Х 9, Х 10 в уравнении (1), й соответственно обозначают нулем, 1218376 2Изобретение относится к автоматике и вычислительной технике, вчастности к программному управлениютехнологическим оборудованием,и может быть использовано в программируемых системах управлениятехнологическими объектами, алгоритм управления которых описываетсяс помощью булевых Функций, в частности в программируемых контроллерах иуправляющих вычислительных машинах.Устройство для вычисления булевыхФункций позволяет вычислять скобочные Формы булевых функций, представленных в виде лестничной диаграммы.Наряду с такой Формой представлениябулевых функций в технике используется представление булевых Функцийв виде компактной записи и в Формеалгебраических уравнений. При этомсуществует необходимость созданияустройства, реализующего любую скольугодно сложную булевую Функцию,представленную в Форме алгебраического уравнения.Цель изобретения - расширение области применения за счет реализации любых скобочных Форм булевыхфункций, представленных в виде алгебраических уравнений.Па Фиг. 1 представлена схема устройства; на Фиг. 2 - схема узла счета.на Фиг, 3 - блок-схема алгоритмаработы устройства.Устройство содержит элемент11 СКЛ 10 ЧЙОЩЕЕ ИЛИ 1, триггеры 2 и 3,узел 4 счета, элементы И 5-8.Узел счета содержит элементыИ 9-10, реверсивный счетчик 11 и дешифратор 12.Нлокц блок-схемы алгоритма работыустройства выполняют следующие дейстгил: блок- установить состояниетриггеров 2 и 3 равное единице,блок 2 - проверить состояние триггера 2 на равенство едшшце, блок 3проверить состояние триггера 3 наравенство единице; блок 4 - проверитьсовпадает ли действительное значениеаргумента со значением аргумента,указанным в управлении; блоки 5 и 6 проверить наличие знака дизъюнкции"+"; блок 7 - установить состояниетриггера 3 равное нулю, блок 8 -установить состояние триггера 2 равное нуло; блок 9 - проверить наличиезнака "Закрывающая скобка" ")";блок 10 - проверить наличие знака1218376 51 О 15,конъюнкция, функции присваивается Действительное значеЗначение Вычисленное значеаргумента, указанное ние аргумента ние аргумента в уравне"нии О О О О 55 если этот аргумент записан со знаком инверсии (аргументы Х 2 и Хб в уравнении (1), При таком обозначении совпадение действительного зна- . чения аргумента и значения аргумента, указанного в уравнении, означает, что аргумент истинен (т.е, его вычисленное значение равно единице), несовпадение этих значений означает, что аргумент ложен (т.е, его вычисленное значение равно нулю). Составляют табл. 1 по результатам этих вычисленийТаблица 1 Как видно из данных табл, 1, для вычисления аргумента можно использовать элемент провеки на четность (ИСКЛЮЧАЮЩЕЕ ИЛИ с инверсией).Если на входы элемента подавать сигналы действительного значения аргумента и значения, укаэанного в уравнении, то на выходе получают вычисленное значение аргумента.В процессе вычисления уравнения существует два условных перехода: когда вычисленный аргумент истинен и после него стоит знак дизъюнкции "+", когда вычисленный аргумент ложен и после него нет знака дизъюнкции (т.е. стоит знак конъюнкции) .В примере - уравнение (1) эдак дизъюнкции стоит после аргументов Х 2, ХЗ, Х 5, Х 7, Х 9. В первом случае процедура условного перехода такова: функции присваивается значение 1, накладывается запрет на вычисление остальных слагаемых дизъюнкций до отыскания последнего аргументами входящего в 20 25 30 35 40 45 50 данную дизъюнкцию, после чего вычисление продолжается.Если уравнение заканчивается последним членом этой дизъюнкции, то результатом решения данного уравнения будет единица.Во втором случае функции присваи. вается значение ноль, накладывает- ся запрет на вычисление остальных сомножителей данной конъюнкции до отыскания последнего аргумента, обнаруживается дизъюнктивный член ,к той части функции, в которую входит только что вычисленная значение 1 и вычисление продолжает" ся. Если уравнение заканчивается последним членом данной конъюнкции, то результатом решения этого уравнения будет О.Эти правила вытекают из предложений булевой алгебры: если в дизъюнкции хотя бы один из слагаемых равен единице, то вся диэъюнкция равна единице, если в конъюнкции хотя бы один из сомножителей равен нулю, то вся конъюнкция обращается в нуль.Устанавливают правило для отыскания последнего аргумента дизъюнкции при первом условном переходе. Для этого рассматривают дизъюнкцию Х 1+Х 2+ХЗ +Хп = У (2).Если эта дизъюнкция входит в состав более сложного аргумента, то она должна быть заключена в скобки /Х 1+Х 2+ХЗ+ +Хп/ а Хп+1=7 (3) или Хп+1 /Х 1+Х 2+ХЗ+ +Хп/Хп+г=т (4) где Хп+1 и Хп+2 - любые, сколь угодно сложные аргументы.Из уравнений (3) и (4) видно, что окончание дизъюнкции определяется наличием закрывающей скобки. Однако любой член дизъюнкции может быть сложным аргументом, в свою очередь содержащим скобкиНапример, Х 2 = Л /Я, + Л/, тогда уравнение (3) примет вид /Х 1+ Л /Л + Л /+ХЗ +Хп/Хп+1 = т (5).При этом по ходу вычисления, ес" ли например Х 1=1-, имеется закрывающая скобка после аргумента 1., которая не характеризует окончание данной дизъюнкции. Такие скобки,принадлежащие сложным аргументам,.характеризуются тем, что каждойзакрывающей скобке соответствуетоткрывающая скобка и лишь последняязакрывающая скобка, указывающаяна конец дизъюнкции, оказывается нескомпенсированной открывающей скобкой. Поэтому правило для отыска. цця последнего члена дизъюнкции можно трактовать так, по ходу вычисления подсчитывается количество открывающих и закрывающих скобок и тот наиболее близкий шаг вычислений, в котором число закрывающих скобок хотя бы на одну больше числа открывающих скобок, указывает на конец дцзьюнкции.Устанавливают правило для отыскапия последнего аргумента конъюнкции при втором условном переходе. Для этого рассматривают коныонкцио Х 1 Х 2 кХЗ Хп = У (б). О 5 40 Если эта коньюнкция вкоцит в состав более сложного аргумента, то после нее должен стоять знак дцзьюнкциц, с помощью которого к пей присоединяется в общем случае любой, сколь угодно сложный аргу ментХ Х 2 ХЗ Хп+Хп+1 Х=у (7)Из уравнения (7) видно, что окончание конъюнкции определяется наличием знака дизъюнкции "+". Од 30 пако каждый из аргументов Х+Хп молот быть сколь угодно сложным, содержащим в свою очередь знаки дцзъюнкциц, Например, Х 2 = Л,+ Л Такие аргументы заключаются в скобки Х 1 "/Л, + Л, /х ХЗХп + Хп+1=У (8)Тогда перед каждым знаком дизъюнкцци, входящим в сомножительФ вычисляемой конъюнкции, должна быть открывающая скобка и лишь в том случае, когда все открывающие скобки скомпенсированы закрывающими скобками, знак дизъюнкции "+" является указанием на окончание коныонкции. Тогда правило для отыскания последнего члена коныонкции можно трактовать так: по ходу вычисления подсчитывается количество открывающих ц закрывающих скобок, причем закрывающие скобки считаются лишь тогда, если имеется хотя бы одна открывающая скобка. Если разность между числом открывающих и закрывающих скобок равна нулю, то наиболее близкий по ходу вычисления знак дцзъюнкции "+" указывает на55 окончание конъюнкции.Элемент ИСКЛ 10 ЧАЮЩЕЕ ИЛИ 1 (фиг, 1) устройства служит для вычисления аргумента. Триггер 2 служит для хранения текущего и вычисленного значения Функции. Выход триггера 2 является выходом устрой ства. Сигнал, снимаемый с этого выхода, есть вычисленное значение Функции. Установка триггера 2 в нулевое состояние определяет начало второго условного перехода. Триггер 3 служит для фиксации первого условного перехода, установка триггера 3 в нулевое состояние определяет начало первого условного перехода.Узел 4 счета служит для подсчета открывающих и закрывающих скобок уравнения в процессе условных переходов. Узел 4 счета (Фиг. 2) может, например, состоять из двоичного реверсивного счетчика 11 и дешцфратора 12. Двоичный реверсивный счетчик имеет входы "Сложение" ц "Вычитание", а также входы установки нуля и синхронизации, Если выходы триггеров 2 и 3 через элемент И 10 соединить с входом установки нуля счетчика, то перевод любого из триггеров в нулевое состояние будет сигналом для начала подсчета открывающих и закрывающих скобок. При этом, если на вход Сложение" подавать сигналы "Открывающая скобка" ")", а на вход "Вычитание" подавать сигналы "Закрывающая скобка" "1" и начинать подсчет закрывающих скобок, если счетчик не находится в нуле, т,е. когда была подсчитана хотя бы одна открывающая скобка, то нулевое состояние счетчика всегда определяет, что по ходу вычисления, все открывающие скобки скомпенсированы закрывающими. При этом можно использовать дешифратор числа = О,Единичный сигнал на выходеэтого дешифратора и наличие по ходу вычисления закрывающей скобки определяют окончание первого условного перехода. В этом случае на обоихвходах элемента И 8 будут единичныесигналы и триггер 3 переведется вединичное состояние. Единичный сигнал на выходе дешифратора и наличие по ходу вычисления знакан иДизъюнкция определяют окончаниевторого условного перехода, приэтом на обоих входах элемента И 7будут единичные сигналы и триггер 2переведется в единичное состояние.Входы установки единицы триггеров - 2 и 3 имеют приоритет над входами установки нуля.Устройство работает следующим образом.Перед каждым циклом вычисления подается сигнал "Установка устройства в исходное состояние", Тригге- ры 2 и 3 устанавливаются в единичное состояние. В процессе вычисления через управляющий вход устройства на вход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1 подается сигнал "Значение аргумента, указанное в уравнении", на входы элементов И 6, 7 подается сигнал "Дизъюцкция", ца вход элемента И 8 подается сигнал "Закрывающая скобка" ") " и на вход узла 4 счета подаются сигналы Открывающая скобка" "(" и "Закрывающая скобка" ")". Эти сигналы подаются в том .порядке, как они записаны в уравне:нии.Когда ца всех входах устройства установятся сигналы, подается сигнал синхронизации, по переднему фронту которого переключаются триггеры 2 и 3 и узел 4 счета. При подаче ца один вход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1 сигнала "Значение аргумента, указанное в уравнении", на другой вход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1 подается действительное значение аргумента. Если эти значения совпадают, т.е.111 на обоих входах будет либо нуль либо "единица", то на выходе элемента будет "нуль", и если есть знак "Дизъюнкция", то триггер 3 переводится в нулевое состояние, так как на входах элемента И 6 будут единичные сигналы. При этом накладывается запрет на вычисление последующих аргументов, так как на входе элемента И 5, соединенном с выходом триггера 3, будет нулевой сигнал. Одновременно узел 4 счета подготавливается к отсчету открывающих и закрывающих скобок. Если по ходу вычисления все открывающие скобки будут скомпенсированы закрывающими скобками и имеется лишняязакрывающая скобка (частный случай,когда между знаком дизъюнкции изакрывающей скобкбй нет ни однойоткрывающей скобки), то на обоихвходах элемента И 8 будут единицыи триггер 3 через вход установки10 единицы будет переведен в единичноесостояние.Если действительное значение аргумента и значение аргумента, указан.ное в уравнении, не совпадают, то15 на выходе элемента ИСКЛЮЧАЮЩЕЕ ИЛИ 1будет единица, и если нет знака"Дизъюцкция", то по входу установкинуля триггер 2 переведется в нулевое состояние. При этом узел 4 сче 2 О та будет подготовлен к отсчету открывающих и закрывающих скобок. Еслипо ходу вычисления все открывающиескобки будут скомпенсированы закрыл 11вающими и имеется знак Дизъюнкция25 (частцый случай, когда после вычисленного аргумента сразу же стоитзнак дизъюцкции), то на обоих входах элемента И 7 будут единицы,триггер 2 будет переведен в единичЗО ное состояние, и вычисление продолжается.После вычисления последнего аргу"мента уравнения значение функции(О или 1) снимается с выхода триг 35гера 2. Это значение является результатом решения уравнения..Рассмотрим пример вычисления конкретной булевой функции, записанной в виде алгебраического уравнения4 О Х 1+Х 2/ХЗ/Х 4+Х 5/+Х 6 д Х 7/+Х 8/Х 9++Х 10/Х 11+Х 12/Х 13+Х 14/+Х 15 = У.Предположим, действительное зна- ечение аргументов ХЗ, Х 7, Х 8, Х 9,Х 13 совпадает со значением аргу 45 ментов, записанным в уравнении,а действительное значение остальныхаргументов - не совпадает. Результаты решения уравнениясведем в табл. 2.(проверяемый аргумент) ние навыходеузла4 счета яниесчетчикаяние яние чие чие триггера 3 закры- тригге"вающей ра 2скобки знака откры"дизъюн вающей кции "+ скобки О Нет 1 Нет О Нет О Нет 0 Есть 0 Нет О Есть 1 Нет 1 Нет Есть Х 1 Е 1 ет Нет Х 2 0. Х 5 0 Нет Хб Есть Еет Х 7 Нет 0+2 Х Х Х 13 О Есть 1 Нет Х 14 Есть 1 Нет Х 15 45 Знак Х обозначает безразличноесостояние.Результатом решения уравненияявляется значение функции У =снимаемое с выхода триггера 2 после50вычисления последнего аргументауравнения. Формула изобретения Устройство для вычисления булевых функций по авт. св. Р 1049898, о т л и ч а ю щ е е с я тем, что, с целью расширения области применения за счет реализации любых скобочных форм булевых функций, представпенных в виде алгебраическихуравнений, выход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ соединен с инверсным входом третьего элемента И, входы синхронизации первого и второго триггеров и реверсивного счетчика соединены с входом синхронизацииустройства, входы установки в исходное состояние первого и второготриггеров соединены с входом установки в исходное состояние устройства.