Цифровой генератор функций

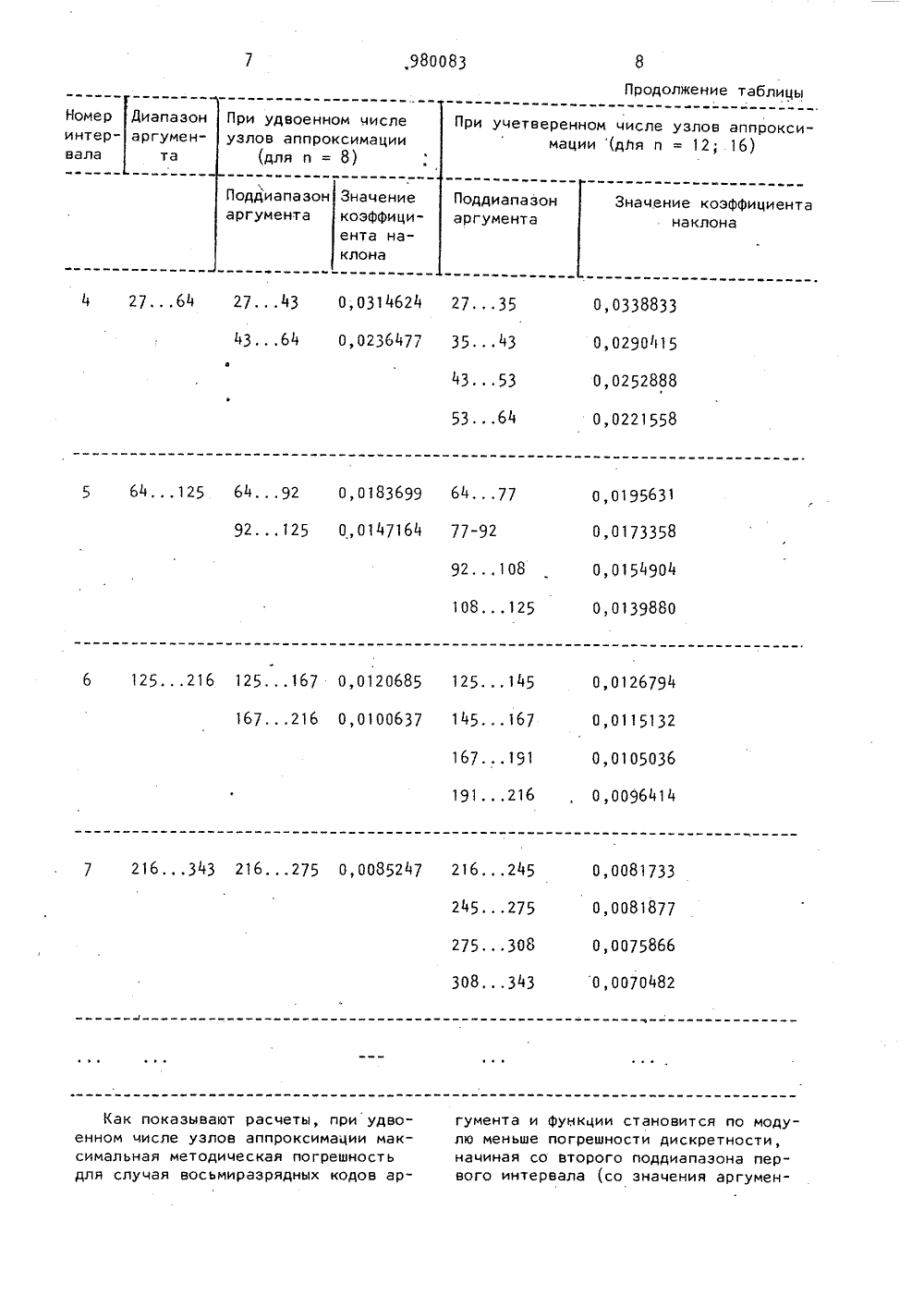
Союз СоветскихСоциалистическихРеспублик ВИДЕТЕ ЛЬСТВУ АВТОРСК(23) СССР ао делам иаооретенкЯ к открытиЯОпубликовано 07.12,82. бюллДата опубликования описания тень %452) Автор изобретения Е илат Новосибирский электротехнический институт(71) Заявите ЦИФРОВОЙ ГЕНЕРАТОР ФУНКЦИЙ Изобретение относится к цифровоивычислительной технике и может бытьиспользовано в цифровых, цифроаналоговых, вычислительных и информационно-измерительных устройствах и системах, а также в устройствах автоматики для формирования разнообразныхФункциональных зависимостей, в томчисле степенных, логарифмических,тригонометрических и пр,Известно устройство с кусочно-линейным воспроизведением функций. Независимо от места формирования управляющих сигналов аргумент представляется в виде число-импульсного кода, а изменение крутизны воспроизводимой функции осуществляется за счетизменения коэффициента деления управляемого делителя частоты, формирующего приращения выходной функции 1 11.Однако при этом набор коэффициентов деления невелик, а абсолютная величина значений крутизны не можетбыть больше единицы. Данные обстоятел.ства существенно ограничивают точностные характеристики устройства.Наиболее близким к предлагаемому.по технической сущности является устройство, содержащее счетчик-регистрмента накапливающии сумматорблок памяти и делитель частоты, приэтом адресная часть блока памяти соединена с выходом делителя частоты,вход которого соединен со входом устройства, входом счетчика-регистрааргумента и тактирующим входом управ,ления выдачей кодов блока памяти, информационные выходы которого соединены с информационными входами накапливающего сумматора. Известное устройство осуществляет кусочно-линейную аппроксимацию воспроизводимойфункции, причем узлы аппроксимации 2 о задаются с постоянным шагом по аргументу. Аргумент, представляемый ввиде число-импульсного кода, подается одновременно на счетчик-регистр ивход делителя частоты с постоянным83 аций, содержащем счетчик, блок памятии сумматор, информационный вход которого соединен с выходом блока памяти,тактовый вход сумматора подключен ковходу генератора, выход переполнениясумматора соединен с установочнымвходом сумматора и счетным входомсчетчика, выход которого соединен свходом старших разрядов адреса блокапамяти, вход младших разрядов адресакоторого соединен с выходом старшихразрядов сумматора,На чертеже представлена блок-схема генератора.Цифровой генератор функций содержит счетчик 1, блок 2 памяти, сумматор 3 и вход 4 генератора.Алгрритм работы генератора рассмотрим на примере Формирования Функцииу = -/х .Целочисленные значения аргументах = 1 и хг, при которых имеютместо целочисленные значения функцииУ = 1 ( = 1 2, 3), различаютсяна величину С"=1 - (1-1):Ь,1 (,1)=1 что дает ряд чисел. 1, 7, 19, 37, 61, 91, 127, , Если при очередных целочисленных значениях х = 1, заключенных в интервале между значениями Р и г (г с 3 сК), задвть функции у приращения равные (2,Е3 1+1)-",то будет Формироваться кусочно-линейное приближение Функции Уравнение отрезков ломаной на 1-ых интервалах аппроксимации может быть записано в видеЗИ) к-г . к 1-(-1) Р-г Ъ р )ъ (2) откуда Во-вторых, для устройства характерно и высокое значение инструментальной погрешности вычислений. Дело втом, что коэффициенты наклона, задаваемые в виде некоторых постоянных чисел, характеризующих приращения функции на данном участке аппроксимации,записываются в блок памяти с некоторойпогрешностью из-за ограниченности разрядной сетки его выходных слов. Таккак за время вычислений общее числосуммирований в накапливающем сумматоре может быть весьма значительным, а 4 фданная инструментальная составляющаяпогрешности непрерывно накапливается,результирующая погрешность вычисленийможет стать недопустимо большой. Ееуменьшения можно добиться только за ф 0счет увеличения разрядности выходныхслов блока памяти и сумматора, чтотакже приводит к резкому возрастаниюаппаратурных затрат.Цель изобретения - повышение точ- Иности воспроизведения функций,Поставленная цель достигаетсятем, что в цифровом генераторе функМетодическая погрешность кусочно-линейной аппроксимации вида (2) равнаЗ Х - (-1)Ъь =1- Гх = .. -(- )-/7Координаты ее максимальных значений внутри интервалов аппроксимации х могут быть найдены, если первую производную, равную-ЦЪ(И)+ З(-1) 3 9800 коэффициентом деления. Блок памяти, при поступлении каждого импульса входного кода подает на сумматор постоянные числа, соответствующие коэффициенту наклона на данном участке аппроксимации. Переход на следующий отрезок ломаной осуществляется по сиг,налу с выхода делителя частоты, при этом изменяется адрес в блоке памяти и на его выходах устанавливается новое 0 значение коэффициента наклона 2),Недостатком известного устройства является низкая точность, обусловленная следующими причинами.Во-первых, из-за того, что интер валы между узлами кусочно-линейной аппроксимации сохраняются постоянными независимо от кривизны воспроизводимой функции, методическая погрешность Формирования функции на некоторых 20 участках может быть значительной. В принципе можно выбрать интервал аппроксимации по условию обеспечения требуемой методической погрешности на самом неудобном участке васпроиз водимой функции с максимальной кри-. визной. Но в таком случае, особенно при малых значениях требуемой методической погрешности, резко возрастает общее число участков аппроксимации з 0 а следовательно, и объем блока памяти коэффициентов наклона.980083 6Как показывают, расчеты по формуле(7), модули максимальной методическойпогрешности на всех интервалах кусочно-линейной аппроксимации вида (2)при выборе вышеуказанных разрядностейаргумента и функции значительно превышают погрешность дискретности рав- .ную 2Иетодицеская погрешность можетбыть существенно уменьшена, еслииспользовать увеличенное количествоузлов аппроксимации, Для практицескойреализации наиболее удобно увеличениечисла узлов, кратное двум, а именнов 2, 4, 8 и т.д, раз. В частности,при удвоенном и учетверенном числеузлов аппроксимации коэффициент наклона изменяется не только на границах 1-ых интервалов с.целочисленнымизначениями х = г и х = Р , но и въ 1ближайших внутренних точках х = 1,при которых становятся справедливыми неравенства у р 11 + 0,5 (для удво"енного числа узлов), либо у1 + 0,25у 1 + 0,5;уЪ 1 + 0,75 (для, учетверенного числа узлов). В качестве примера в нижеследующей таблице приведены границы поддиапазонов аргументаи значения коэффициентов наклона дляпервых семи интервалов целочисленныхз,значений Функции у = -1 х при удвоенноми учетверенном количестве узлов аппроксимации. х =1(1-1) +(1-1)+- 3 76)1 Фднах 3 При подстановке (6) в (4) получается д,о =(-)0-1) феСО)+6-1)"фРОЙ(7)юоМетодическая погрешность аппроксимации имеет отрицательный знак, а абсолютная велйцина ее максимальных значений уменьшается с ростом 1.В практике вычисления или Формирования функций наиболее типична.ситуация, при которой приведенную погрешность результата необходимо иметь равной или близкой к приведенной погрешности задания аргумента. Число значающих разрядов, функции принимают при этом равным числу значащих разрядов аргумента. В частности,при изменении корня третьей степени из аргумен" та, имеющего диапазон х х щах = = 2 -1 необходимо иметь в = 11 оц ,3 хщ. разрядов для представлейия целой части (здесь 11, - ближайшее боль. шее или равное целое число). и р = и-в разрядов для представления дробнойзв части результата. При и = 8, 12, 16 значения в и р равны соответственно в =. 3, 4, б; р = 5, 8, 10,При удвоенном числе узлов аппроксимации(для и = 8) При, учетверенном числе узлов аппроксимации (для и = 12; 16)Номер Диапазон интер аргумен вала та Поддиапазон Значение аргумента коэффициента наПоддиапазонаргумента клона 1,0 0,2599210(0,2211248)0,1637400(0,14515155) 24(3,4) 4 8 0,1031497 0,1148598 0,0814397 46 68 3 827 8;16 0,0649803 1627 0,0436507 0,0516034 0,0478164 0,0401793 121616 ;21 21,.;27 5приравнять нулю. Отсюда 01- 1,0 2 18 14 О, 1958004980083 Продолжение таблицы При учетверенном числе узлов аппроксимации (для и = 12;.16) Номеринтервала Диапазон аргумен- та При удвоенном числе узлов аппроксимации(для и = 8) Значениекоэффициента наЗначение коэффициента наклонаПоддиапазонаргумента Поддиапазонаргумента клона 27, ,64 2743 0,0314624 27 .,35 4364 0,0236477 3543 4353 53 ,.64гумента и функции становится по модулю меньще погрешности дискретности,начиная со второго поддиапазона первого интервала (со значения аргуменКак показывают расчеты, при удвоенном числе узлов аппроксимации максимальная методическая погрещность для случая восьмиразрядных кодов ар 0,0338833 0,0290415 0,0252888 0,0221558 0,0126794 0,0115132 0,0105036 0,0096414 0,0081733 0,0081877 0,0075866 0,00704829 9800та равного четырем), т. е, на 61(64.диапазона аргумента ее влиянием наточность устройства можно пренебречь,Для случая двенадцати- и шестнадцатиразрядных кодов аргумента и функции 5значение максимальной методической погрешности на всех интервалах аппроксимации с удвоенным числом узлов неуходит за пределы разрядной сеткии необходим переход к большему чис флу узлов, В частности, при учетверенном числе узлов модуль максимальнойметодической погрешности становитсяменьше погрешности дискретности длядвенадцатиразрядных входных и выходных кодов, начиная со второго поддиапазона третьего интервала (со значе.ния аргумента равного ч 3), т. е,на 6 ЯМдиапазона аргумента, а дляшестнадцатиразрядных входных и вы фходных кодов - начиная с пятнадцатого интервала со значения аргумента равного 3375), т. е. на 19/20 диапазона аргумента. Если в последнемслучае необходимо обеспечить методическую погрешность аппроксимациипренебрежимо малой на большем участке значений аргумента, то необходимоосуществлять дальнейшее увеличениечисла узлов. зоПри практической реализации вышеизложенного способа кусочно-линейной аппроксимации приращения функции, задающие коэффициенты наклонана каждом участке, могут быть записаны в блок памяти, управляемый поадресным входам кодом целой частирезультата, совместно по старшимиразрядами дробной части, формируемым в накапливающем сумматоре приращений функции, выход переполнениякоторого соединен со счетным входомсчетчика. Для удвоенного числа узловаппроксимации используется выходтолько старшего разряда сумматора,сигнализирующий о переходе кодарезультата через значение 1 + 0,5,а для учетверенного числа узловстаршего и предыдущего по старшенст- .ву разрядов сумматора, сигнализирующие о переходе кода результата через значения 1 + 0,25;+ 0,5;+ 0,75,Разрядности выходных слов блокапамяти и накапливающего сумматораприращений определяются допустимойинструментальной погрешностью вычислений, Если для представления дробной части результата использовать 83 10число разрядов, выбранное из условия равенства приведенной погрешности задания аргумента и функции, то инструментальная составляющая погрешности не должна превышать единицы младшего разряда, а именно 2 . Число разрядов Ч сумматора, обеспечивающее данное значение инструментальной погрешности, определяется из следующих соображений. Как извест но, при многократном суммировании равноточных чисел абсолютная погрешность возрастает в о раз, где с 1- число суммирований. Если после сформирования очередного переполнения сумматора, т. е. попучения приращения целой части, в сумматоре каждый раз устанавливать определенное, неизменяемое в процессе вычислений значение начального кода, то накопленная на интервале аппроксимации инструментальная погрешность будет периодически устраняться, При этом условии максимальное число суммирований с накоплением погрешности в заданном диапазоне аргумента будет иметь место на последнем полном интервале кусочно-линейного приближения функции с. целочисленными узлами, В частности, при и = 8, 12, 16 с 1 оу равно соответственно 91, 721, 1681, .а сумматор должен иметь не менее= 3 1.од 2 с 1 сл дополнительных разрядов, Для указанных значений и и =10, 13, а общее число разрядов сумматора Ч = и + р будет равно 12, 18, 23 соответственно. Чтобы обеспечить при работе устройства правильность переходов на очередные поддианазоны кусочно-линейного приближения в расчетных узлах аппроксимации, необходимо соблюдать определенную процедуру определения двоичных кодов коэффициентов наклона, подлежащих записи в блок памяти, а также задавать необходимое значение начального кода сумматора, По результатам моделирования различных вариантов определения кодов коэффициентов наклона выбран следующий алгоритм: на первых половинах интервалов аппроксимации между целочисленными узлами коды коэффициентов наклона следует брать по правилу симметричного округления с учетом значения старшего отбрасываемого разряда, а на вторых половинах интервалов - с добавлением единицы младшего11 98008разряда к кодам коЭффициентов наклона, определенным по способу обычногоусечения неучитываемых разрядов, Чтоже касается начального кода, устанавливаемого в сумматоре после сформирования очередного приращения целойчасти, то он выбирается из следующихсоображений. Так как за счет округления коды коэффициентов наклона напервых половинах интервалов в самом 10неблагоприятном случае могут задаваться с отрицательной погрешностью,близкой по модулю к половине погрешности дискретности, а именно х 2 Ффто после самого большого числа сумми- ) .рований, имеющего место на первой.половине старшего, полного интервала,и равного приблизительно 0,5 сщах.абсолютная погрешность недобора ксередине интервала может достигать 20значения 2: 0,5 оп,о2 " . хх 2 Р-: 2" + . Если значениеу, соответствующее узлу аппроксимации в середине -го интервала оценьблизко к 1 + 0,5, то вследствиенакопившейся погрешности недоборапереход на новый поддиапазон аппроксимации может осуществляться не врасчетной точке х = к , а в следующейх = к,(+1, что приведет к потере одно- ЗОго шага аргумента и появлению дополнительной погрешности. Чтобы этого непроисходило, в качестве начальногокода сумматора следует брать число,равное 2 (" ц 1 = 2 , В частности,дпри Ч = 12 и и = 7 5 = 7; при Ч = 18и и = 10 5 = 10; при Ч = 23 и И = 13Ь = 15.Так как максимальный коэффициент наклона, подаваемый на сумматор на40 первом интервале аппроксимации, равен единице, то число разрядов С выходных слов блока памяти должно быть равно разрядности накапливающегосумматора; при этом в ячейке с нулевым адресом должен быть записан код, содержащий во всех разрядах единич .ные значения. Но число й может быть уменьшено, если допустить некоторое увеличение погрешности аппроксимации О на начальных интервалах. В частности, если в исходном состоянии во всех разрядах сумматора установить не нулевые, а единичные значения, то переход на второй интервал аппроксимации И при поступлении первого входногоимпульса осуществится при любом не равном нулю содержимом ячейки с нуле 12вым адресом. Начиная со второго интервала, максимальный коэффициент наклона, подаваемый на сумматор при с одинарном или удвоенном числе узлов,не превышает 0,25, т. е. имеет в двоичном представлении старшую значащую цифру только во втором разряде после занятой. При учетверенном числе узлов он несколько превышает 0,25, но с помощью изменения коэффициента узловаппроксимации на первых поддиапазонах второго интервала все коэффициенты наклона можно сделать меньшими 0,25 (рекомендуемые коррекции отражены в таблице в. круглых скобках), Если учесть данные соображения, то числозначащих разрядов выходных слов блока памяти достаточно иметь равным 1 = У 2, т,е, 10, 16 и 21 соответственно.Устройство согласно предлагаемому изобретению работает следующим образом.В исходном положении все разрядысчетчика 1 устанавливаются в нулевое,а сумматора 3 - в единичное состояние,На выходах блока 2 памяти присутствует любой яе равный нулю код. Аргументподается в число-импульсном коде навход 1 устройства. После поступления первого импульса на тактирующий входсуммирования накапливающий сумматор 3 переполняется и сигнал переполнения поступает на счетчик 1. В счетчике устанавливается код второго интервала аппроксимации, а на выходах блока памяти - код, соответствующий коэффициенту наклона на первом поддиапазоне второго интервала, Сигналпереполнения поступает также на вход установки начального кода сумматора.По мере поступления последующих импульсов входного кода к начальномусодержимому сумматора добавляютсякоды приращений функции на втором интервале аппроксимации, пока не сформируется второе переполнение. В тех промежуточных точках, при которых в сумматоре Формируются значения старших разрядов дробной части результата, соответствующие выбранным точкам перехода на очередные внутриинтервальные поддиапазоны аппроксимации, коэффициенты наклона изменяются в соответствии с расчетными. Второй сигнал переполнения сумматора 3 устанавливает в счетчике 1 код третьего интервала аппроксимации, а в са.мом сумматоре - значение начального кода, На выходах блока памяти ус14 Формула изобретения КИПИ Заказ 9360 ираж 731 Подписно филиал ППП "Патент", .Ужгород,ул.Проектна 13 9800танавливается. значение кода коэффициента наклона на первом поддиапазонетретьего интервала. В дальнейшемработа устройства осуществляется аналогично; при этом в а-разрядном счетчике 1 будет формироваться код целой части, а в р старших разрядахнакапливающего сумматора 3 - достоверные значащие цифры кода дробнойчасти результата вычислений.10Цифровой генератор функций можетбыть использован не только для формирования функции у = / х, но и других монотонных функций, прежде всегостепенных и логарифмических. Более 1того, если счетчик и накапливающийсумматор выполнить реверсивными, причем управление реверсом осуществлятьпо условию достижения кодом в счетчике каких-либо заранее заданных 20значений, то предлагаемое устройствоможет формировать и немонотонные1, в том числе периодические, напримертригонометрические) функции. При этомкаждый раз исходя из .диапазона аргу Змента и требуемой приведенной погрешности воспроизведения функции необходимо предварительно расчетным путем определить интервалы аппроксимации, количество поддиапазонов, коэффициенты наклона на всех участкахаппроксимации, числа разрядов операционных устройств и т,д,При формировании некоторых функцийособенно в случаях, когда требованияк погрешности устройства не слишкомжесткие, разбиение интервалов аппроксимации на поддиапазоны может не по-,требоваться, В таком случае устройство упрощается, так как при этом исклющчаются связи старших разрядов накапливающего сумматора с адресными входами блока памяти и уменьшаются число и разрядность запоминаемых в блоке памяти коэффициентов наклона.Важным практическим достоинством предлагаемого генератора является то, что все его блоки могут быть полностью реализованы на микросхемах высо" кого уровня интеграции. Цифровой генератор Функций, содержащий счетчик, блок памяти и сумматор, информационный вход которого соединен с выходом блока памяти, о т л и ч а ю щ и й с я тем, что, с целью повышения точности воспроизведения функций, тактовый вход сумма- тора подключен к входу генератора, выход переполнения сумматора соединен с установочным входом сумматора, и счетным входом счетчика, выход которого соединен с входом старших разрядов адреса блока памяти, вход младших разрядов адреса которого соединен с выходом старших разрядов сумматора. Источники информации,принятые во внимание при экспертизе1. Авторское свидетельство СССР К УМВБ, кл. С 06 Г 1/02, 1976.2. Клебанский Р.Б., Симаев С.Ш. и Барбакадзе Б,Ш. Разработка дискретных функциональных преобразователей на микроэлектронной базе.,Материалы 1 Всесоюзного симпозиума "Проблемы создания преобразователей формы информации", "Наукова думка", 1976, с. 157- 160 (прототип).