Способ определения реологических параметров линейных вязкоупругих сред при четырех видах однородного нагружения

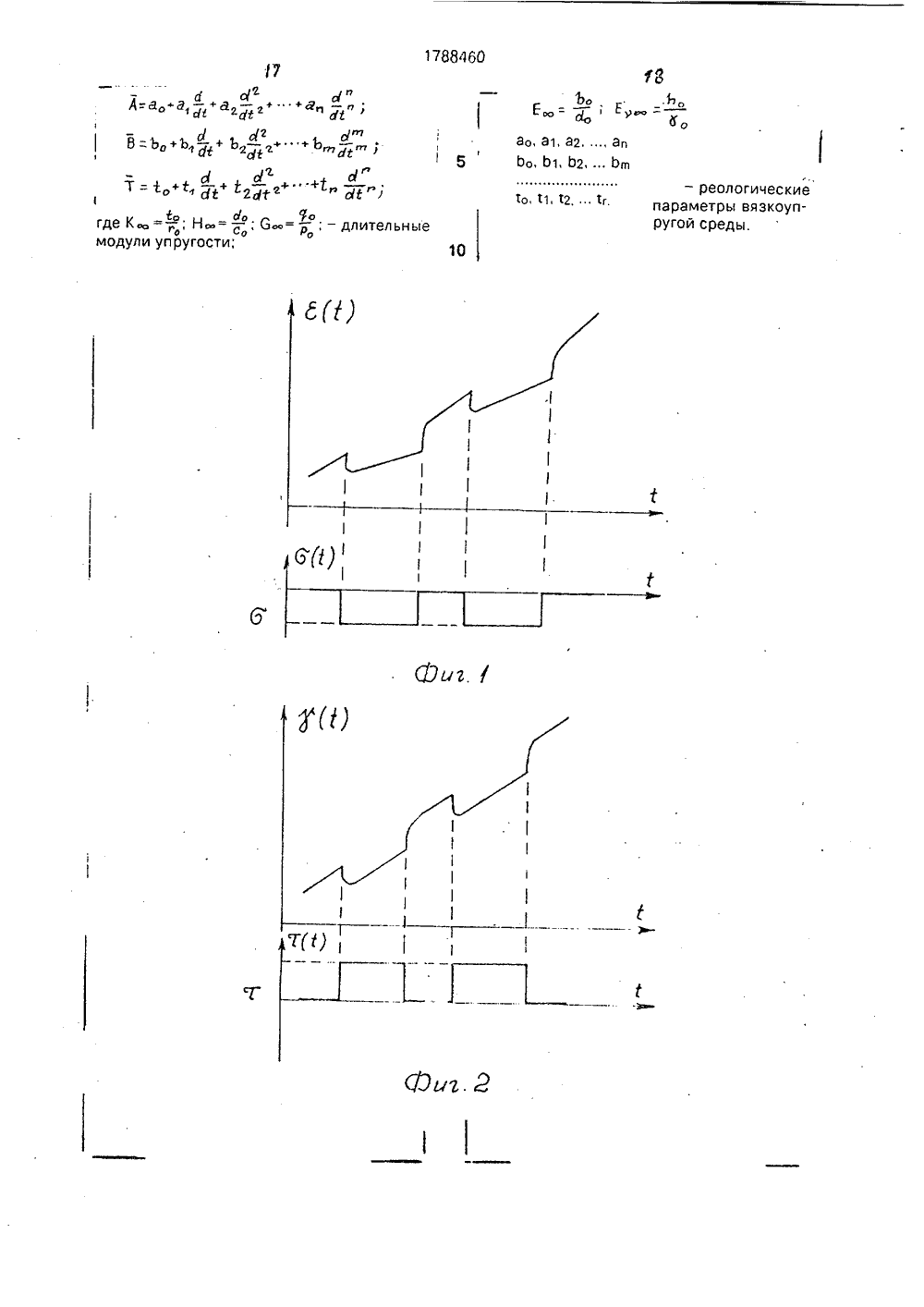
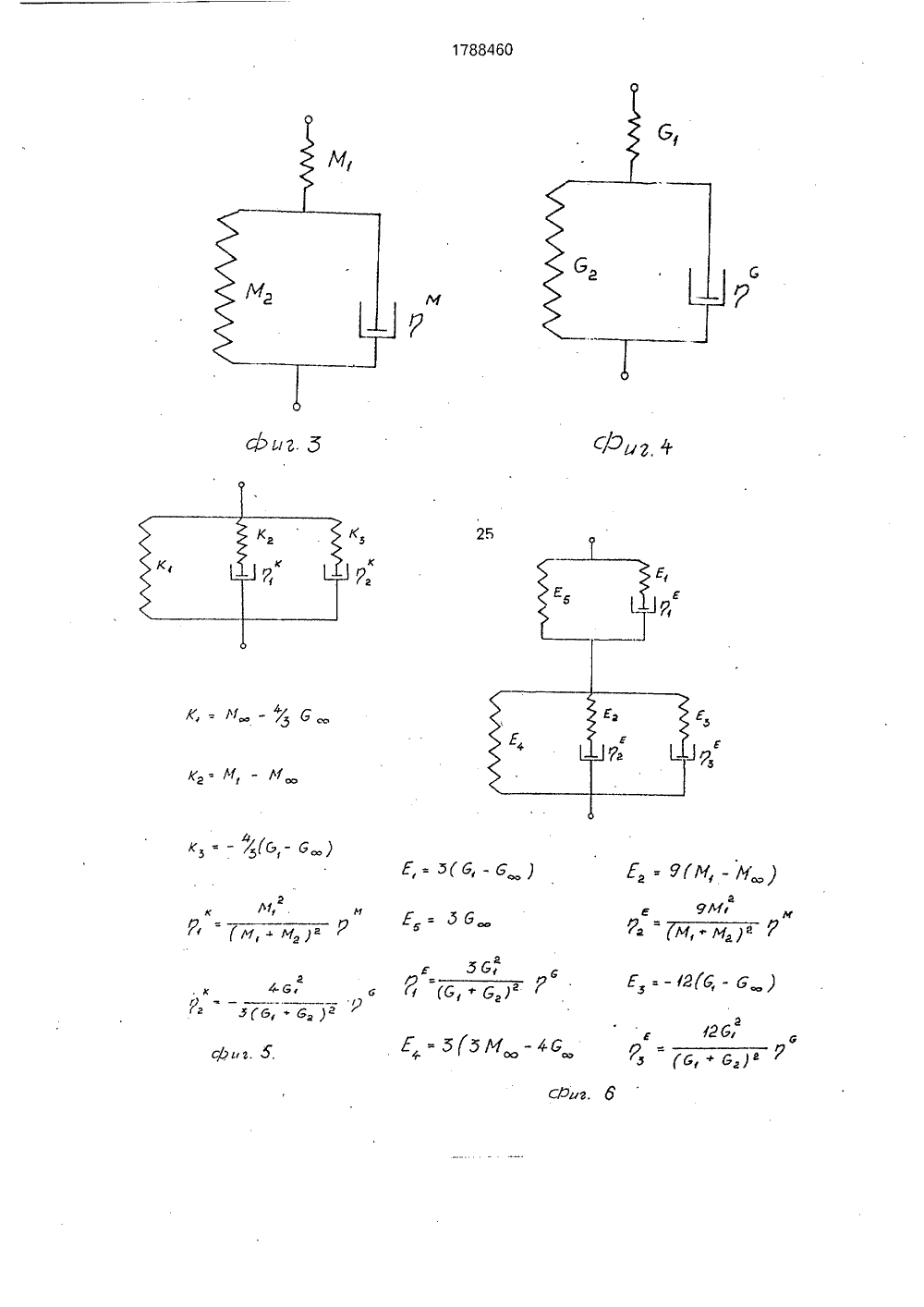
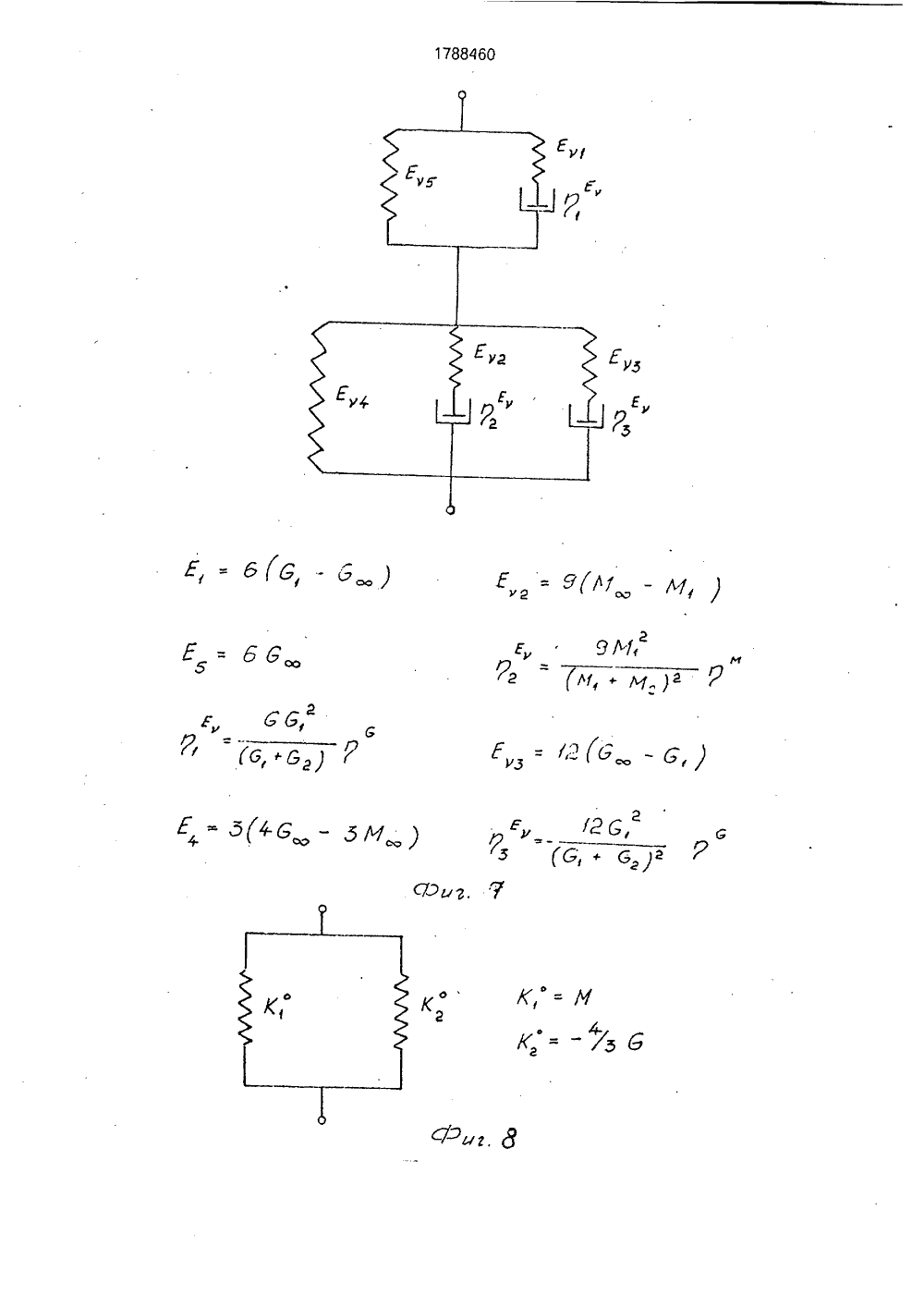
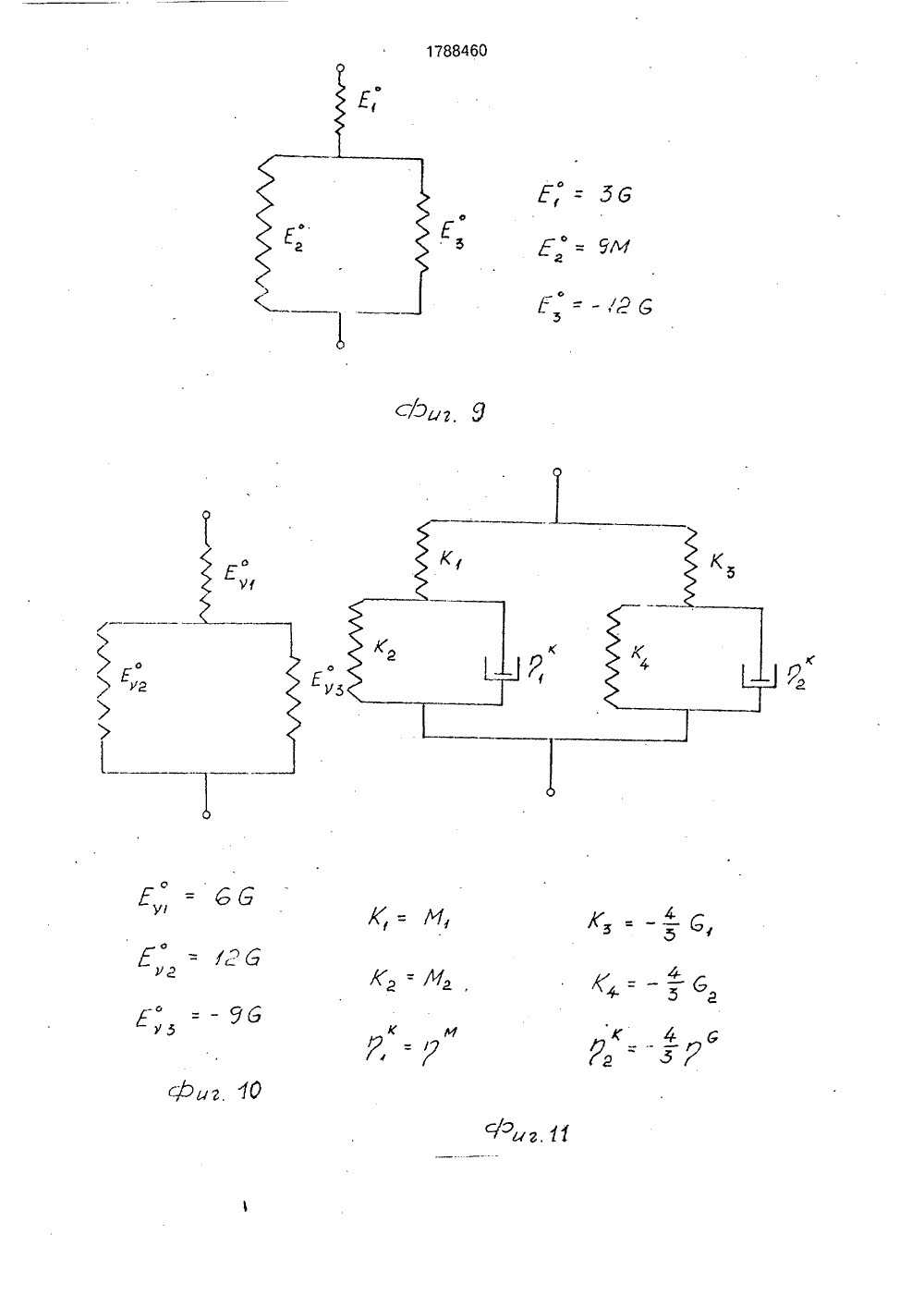
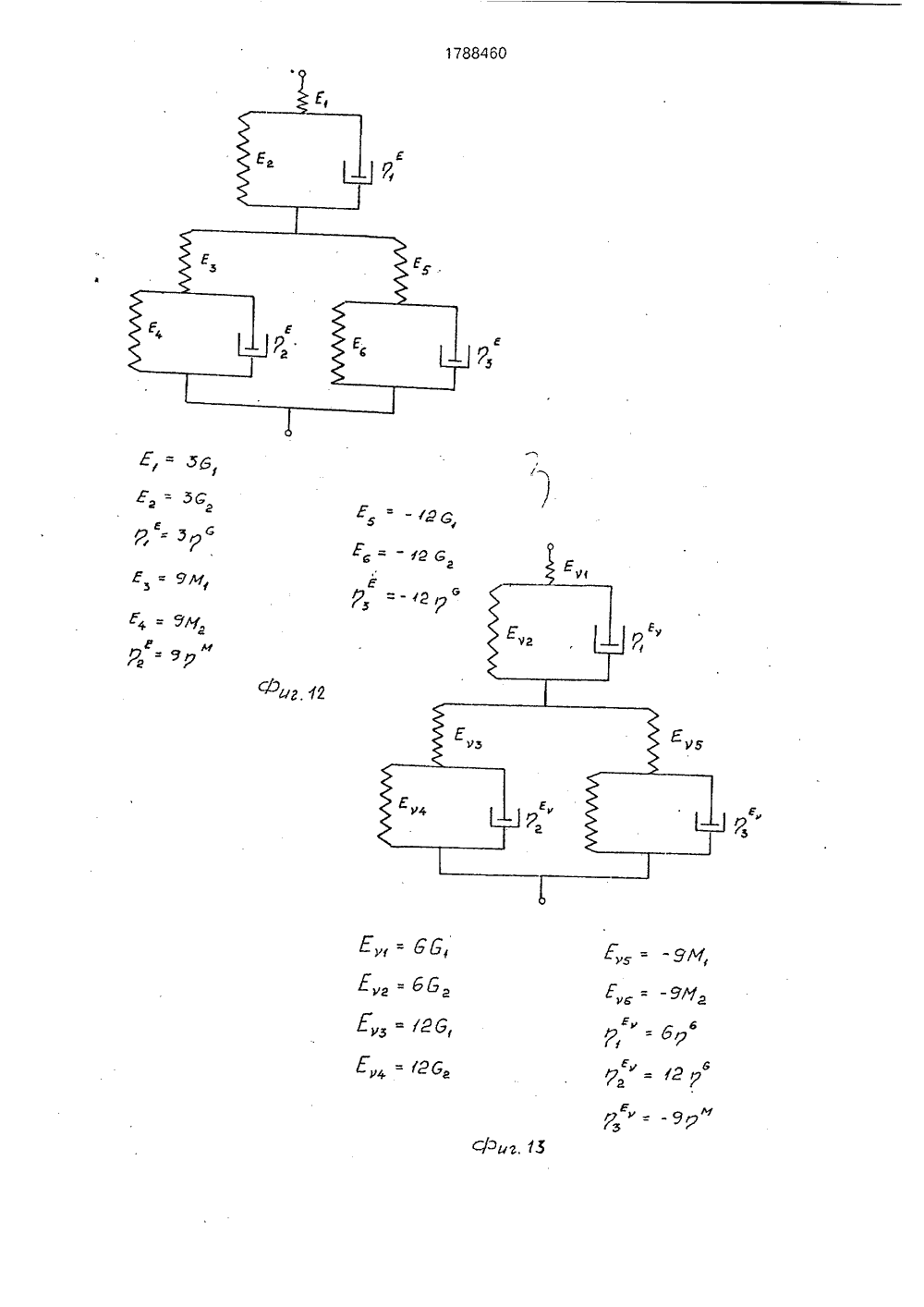
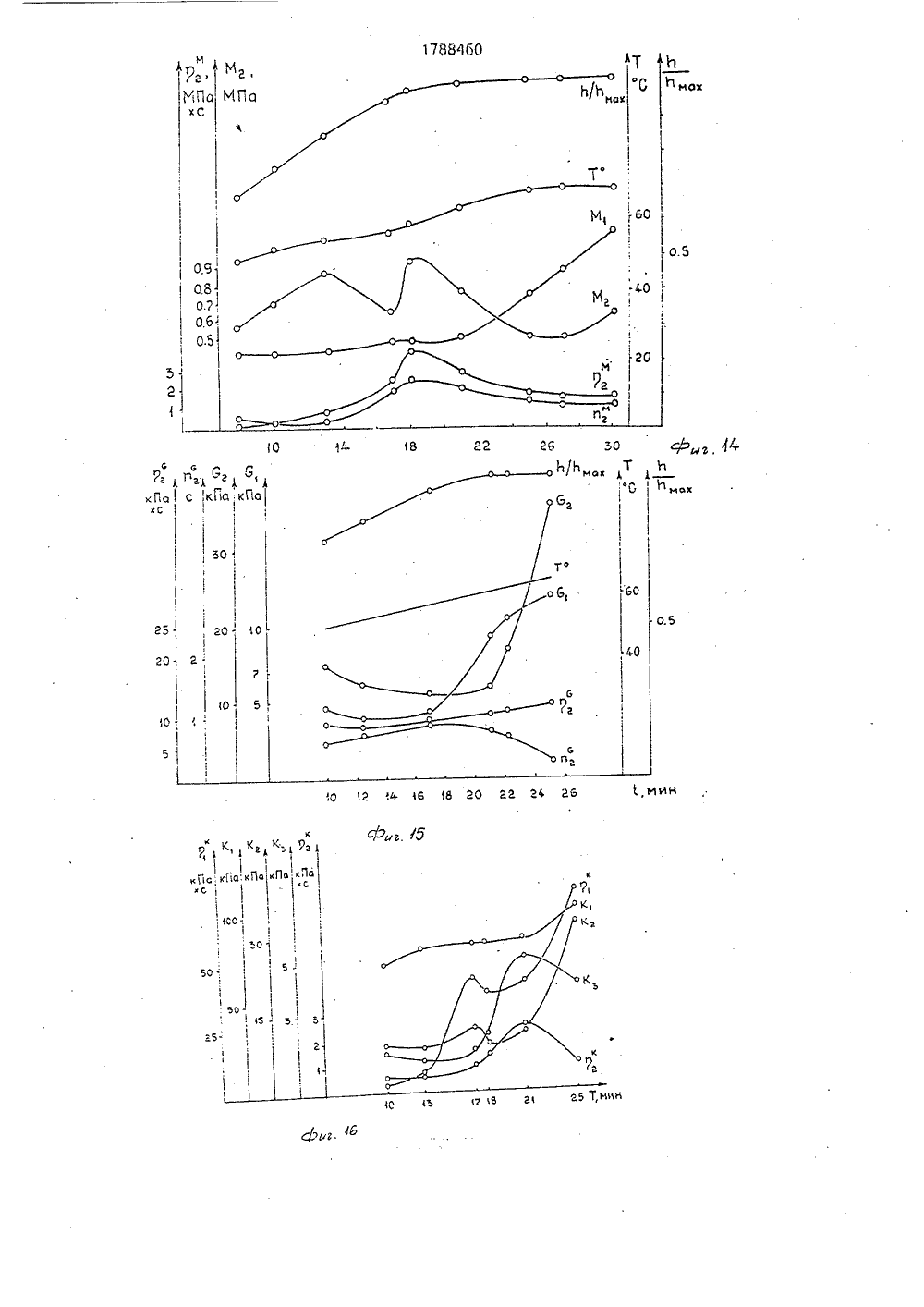
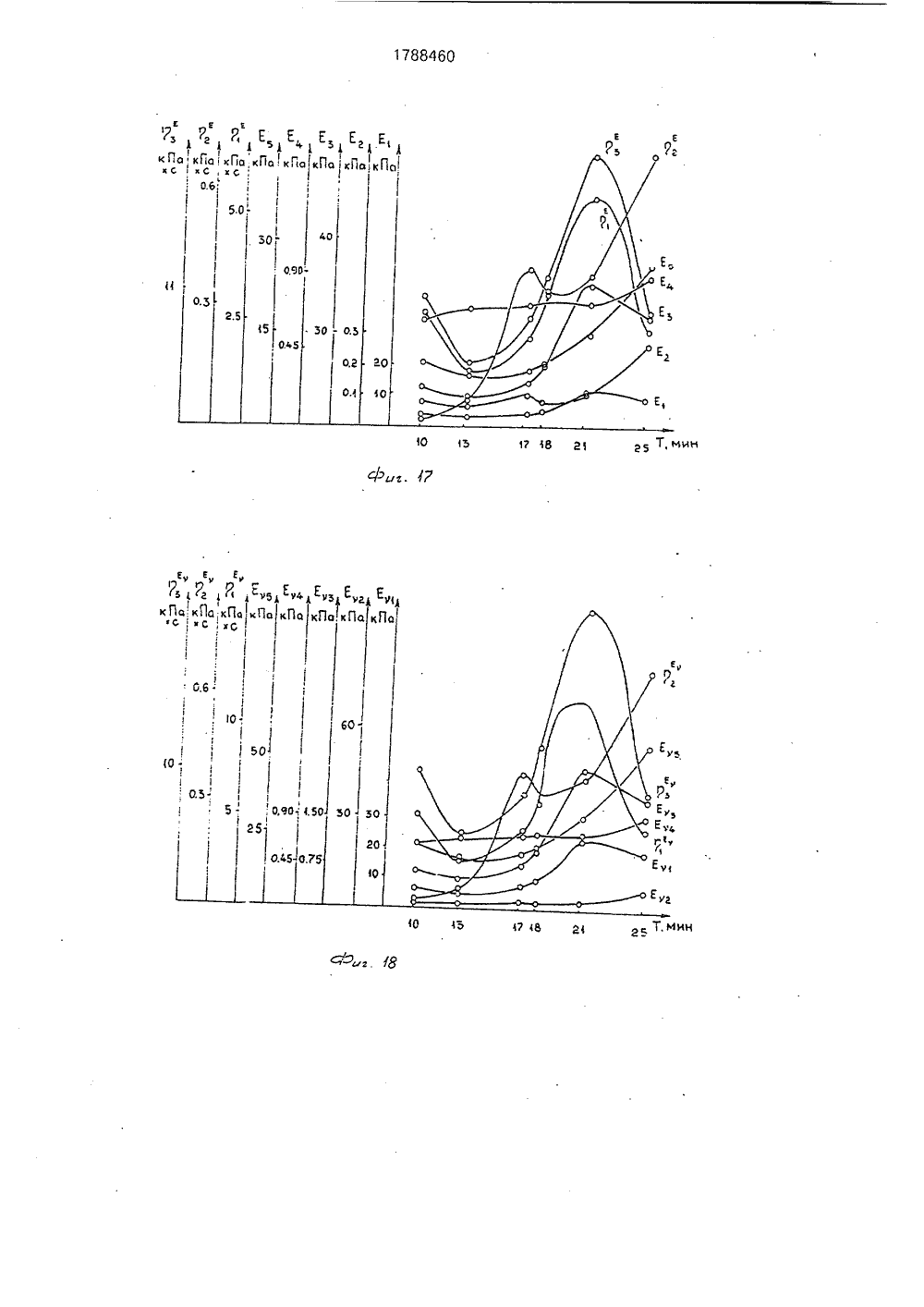
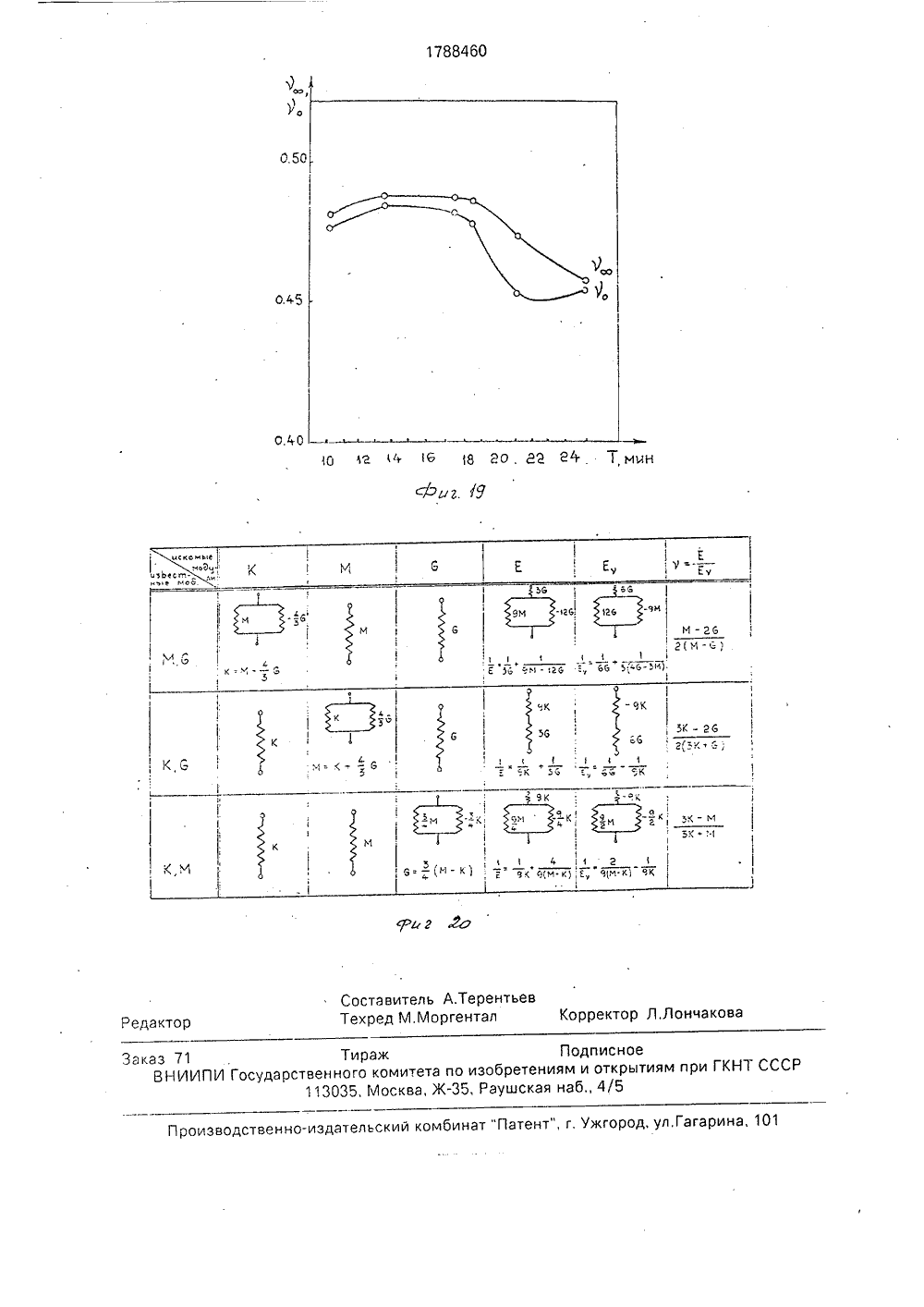
(19) (1 5 001811/О ИСАНИЕ ИЗОБРЕТЕН Я РЕОЛОГИЕЙНЫХ ВЯЗЫРЕХ ВИДАХ ИЯания механисред, наприСущность осуществляют лзучести и опогических паОил,ова-Чумакова Л.В, е (вязкостно-элаоров полимеров и кн.; Успехи химии Сб. 2, М 1957, с. р про- иборе х экс- исслеющейих паф10 с,ГОСУДАРСТВЕННОЕ ПАТЕНТНОЕВЕДОМСТВО СССР(71) Рижский технический университет(56) Куннос Г.Я, Реологические модели телас различным поведением при нагружении иразгрузке. В кн,; Технологическая механикабетона, Рига. Риж.политехн,ин-т, 1978, с. 5273,Реби нде р П.А., И ва н Структурно-механически стические) свойства раст методы их измерения, В и технологии полимеров 146 - 170,Изобретение относится к области исследования механических свойств вязкоупругих сред, например строительных растворов, смесей, в том числе ячеистобетонных, и может быть использовано при оптимизации технологических процессов изготовления строительных материалов и изделий, а кроме того, при исследовании пищевых масс, грунтов, полимеров и т,п.Известны способы определения реологических параметров вязкоупругих сред при каждом из четырех основных видав однородного нагружения, заключающиеся в проведении четырех независимых экспериментов:- трехмерное объемное нагружение, например трехосное сжатие в стабилометре;- одномерное нагэужение, например, компрессионное сжатие в одометре- одноосное нагружение, например одноосное сжатие или растяжение на разрывной машине;(54) СПОСОБ ОПРЕДЕЛЕНИ ЧЕСКИХ ПАРАМЕТРОВ ЛИН КОУПРУГИХ СРЕД ПРИ ЧЕТ ОДНОРОДНОГО НАГРУЖЕН (57) Использование: исследо ческих свойств вязкоупругих мер ячеистобетонных, изобретения: определение путем снятия двух кривых по ределения недостающих реал раметров расчетным путем, 2- сдвиговое нагружение, наприме стой сдвиг в приборе Толстого или пр Вейлера-Ребиндера,с последующей обработкой полученны периментальных кривых ползучести дуем ого материала, позволя определить комплекс его реологическраметров.Известные способы требуют проведения четырех независимых экспериментов нэ четырех различных приборах, что является очень трудоемким процессом, особенно, если требуется синхронизация экспериментов по времени для среды, меняющей свойства во времени, например при твердении. Кроме того, для некоторых видов материалов трудно или невозможно осуществить отдельные виды однородного нагружения, например; одноосное нагружение жидких сред, или всестороннее сжатие для вспучивающихся сред, таких кэк газобетонная смесь,Составительедактор Техред М,Мо Корректор Л.Лончаков аказ 71 Тираж Подписное ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ ССС 113035, Москва, Ж, Раушская наб., 4/5 оизводственно-издательский комбинат "Патент", г, Ужгород, ул,Гагари А.Терентьевргентал гс17884 бО или или га сравнивая с Ц 45лР=ЗК О,(23) Кривой ползучести ф) (фиг. 1) соответствует реологическая модель стандартного линейного вязкоупругого тела, показанная на фиг, 3, и описываемая уравнением;ст+ п 1 о = М Я+ М 1 п 1 е, (11)м М(12) где е - относительная одномерная деформация;0- напряжение;м пг" М,п 1М 1- время релаксации;пг = д /Мг - время ретардации;мМ 1 МгМ = +- длительный модульМ 1+ М 2упругости;М 1, М 2 - мгновенный и задержанный модули упругости;- вязкость задержанной упругоМ сти,Значения указанных величин определяются на экспериментальной кривой фиг. 1 по известной методике.Экспериментальной кривой ползучести у (1) (фиг. 2) соответствует реологическая модель стандартного линейного вязкоупругого тела, показанная на фиг. 4 и описываемая уравнениемт+п 1. =О.у +01 п у,(13)616(1+п 1 - )т =6 (1+п 2 - )у6 б 6 ббт йМгде г - напряжение сдвига;у - относительная деформация сдвиО 126 = +- длительный модульупругости;01 - мгновенный модуль упругости;62 - модуль задержанной упругости;Д пг0 аП 1а 1- время релаксации;п 2 = г/г- Иг - время ретардации;С1) - вязкость задержан ной уп ругости,6 Значения указанных величин определяют из экспериментальной кривой фиг, 2 по известной методике.Определение реологических параметров моделей для остальных двух видов нагружений и коэффициента поперечной деформации возможно провести двумя путями: 1. Экспериментально полученные зависимости представляются в оперативнойформе,5 В рассматриваемом случае это зависимость между напряжением д и деформацией е для одномерного нагружения, Воперативной форме она имеет вид:0 =МЕ., (15)10 где М = Мо О/С,или Со =М О е . (16)Раскрывая операторы по формулам (10),имеем;о ф. п15а( 2иугп20 и, сравнивая с (12), видим, чтос =0 при 1 ъ 2,б=Опри ) 2,б бт.е, С = Со + С 1 - ; О = бо + б 1 - ; (17)бтбт25 асо=1 бо=1 (18)С 1 = п 1; б 1 = п 2м,Оперативная форма зависимости между напряжением и деформацией для простого сдвига выглядит следующим образом:30 т=О у, (19)где 6 = ОО/Р,или Р т - 0 0 у . (20)Раскрывая операторы по формулам (10) 35 имеем; р +Р 1 - р ++ Р ):а со "ф р "фкс а,Р ,40 о/1 4 1 а(1"= 0 при 2,бР 1 - ; 0 = Цо + С 11 - , (21)бт б 1 Ро= 1; Цо; (22) Р 1= П 1 Ц 1= П 2С; 6Таким образом, операторы М и Й опреде лены,Далее по формулам (1), (2), (3), (4) определяются операторы К, Е, 1, 1, т.е. операторы Я, Т, А, В, Г, Й и их коэффициенты г ть а, Ь;1 ь Ь, которые и являются искомыми реоло гическими параметрами.Связь между напряжениями и деформациями в оперативной форме для трехмерного нагружения записывается в следующем виде:11 11 ф врттЕ)1 исие 1 - я(Е)тЕ) -Е) тЕ) ее)в 1 к тппвп =Е)кГтвЕт(ЕЛ Ц -Г) 1 пв+сЕ +Е 5(ЕФфЕ 1 п Е (Е 1,4 Е 51 Й 1 ц+ +Е,Ж +0;Е,1 лгпиаф (Е 4+Е 5 ФИс 1 Е -Еа 1,о пав(Е) тЕ)(Е) тЕ) 1 и,п 1 ок.в е5М( ФМ гдеЕ)Еу Евт Сравнивая коэффициенты при соответствующих членах уравнений (47) и (48), получим искомые значения коэффициентов:6 ,-п=)1, ) п- пМ Е,ж Ц (,- 1, Е =-ч(м,-м Е =-2(С,-С Е)=- Ъ(59 ро, 1, 5 Еу б СИО)2Е а к -ткмт м(м, + м,1Еу 12 бр, )ас,)Для коэффициента поперечной деформации уравнение (3) в операторной форме с учетом (17), (21) и (18), (22) примет вид,гг )л л л м-гс, М.,йр-К ас 2е-М 2(М 2 р-С лл л)1Мое-Ы, в(Мт 2 С 1 и, е (МоеС,1 п,1 Р е(М,-ЯС,1 й, , Р ж ЕМ -С емт-С Д 1 П,+(М -Ц в(Мт-с)1, )л, - ,Коэффициенту поперечной деформации нельзя поставить в соответствие реологическую модель, поскольку он сам является отношением дробно-линейных операторов (4), каждыи иа которыя описывается сваей рео.логическОи моделью, 10 М - 2 6 соУоД(51) При проведениидвух других пар экспериментов, ход рассуждений аналогичен изложенному, поэтому не приводится.2, Соотношения (1), (2), (3), (4) представляются в виде структурных моделей, т.е. цепи последовательно и параллельно соединенных элементов упругости,Согласно символическому методу расчета условной жесткости сложных реологических моделей, по которому жесткость В двух параллельно соединенных элементов В 1 и Вг равна их суммеВ=В 1+Вг (52) а величина, обратная жесткости В двух последовательно соединенных элементов В 1 и Вг. определяется как сумма их обратных величин:1/В = 1/В 1+ 1/Вг (54)соотношения упругости (1 - 4) преобразуются к сумме модулей упругости или их обратных величин.Тогда формула (1) примет вид: К = М+ (-4/3 8) = К 1 .). Кг", (54) 40 т,е. мы имеем параллельное соединениеэлементов с жесткостью К 1 = М и Кг ==(-4/3 О ), показанное на фиг. 8.Формула (2) примет вид:45 + д 1 гр - о) (5 ит.е. имеем последовательное соединениеэлементов с жесткостью Е 1 О = ЗД и жесткостью Е =9 М -126, которую в свою очередьоможнопредставить как параллельное сое динение жесткостей Его = 9 М и Езо = -126(3), получим26 Г -ЖЕуее М - гС55которая преобразуется в структурную формулу вида:1Е," б др,0, рч) Я + с) Г 57) 788460 12Из уравнения (50) можно получить важные для практического применения величины длительного коэффициента поперечной деформации 1, равного отношеник свободных членов в числителе и знаменателе (50), и мгновенного 1 равного отношению коэффициентов при максимальных производных числителя и знаменателя (50).В данном случае55 Посредством поршня смесь подвергалась одномерному нагружению по стандартной методике в сосуде прибора, При этом использовался режим периодического мгновенного нагружения, выдержки под на 13 17т.е. имеем последовательное соединениеоэлементов с жесткостью Е 1 = 66 и жесткоостью Е = 3(40 - ЗМ), и которую в своюочередь можно представить как параллельное соединение жесткостей Е 1 = 120 и Е 1=9 М (фиг. 10).Суммарныежесткости моделей, изображенных на фиг, 8, 9 и 10 посчитанные символическим методом. совпадаютсоответственно с соотношениями (1), (2) и(56).Заменяя упругие элементы фиг. 8, 9 и 10на реологические модели (фиг, 3, 4), подобранные на основе экспериментальных кривых, получают искомые реологическиемодели (фиг. 11, 12, 13) и их параметры,Отметим здесь также, что реологические модели фиг. 11, 12, 13 можно упроститьс помощью эквивалентных замен и свестиих, например, к моделям соответственнофиг. 5, 6, 7, уравнения которых эквивалентны уравнениям моделей фиг, 11, 12, 13,Коэффициенту поперечной деформациинельзя поставить в соответствие реологическую модель, т.к. Он является отношениемдеформаций (см. (4, Е го можно определить,как отношение поперечной деформации Я,полученной из решения уравнения моделифиг, 13, к продольной Я . полученной изрешения уравнения модели фиг, 12 (при 6 ==сопзт).Аналогично можно получить структурные модели и коэффициент поперечной деформации при различных сочетаниях двухизвестных из экспериментов модулей упругости (см. фиг, 20), а следовательно, и искомые реологические модели и их параметры.Здесь следует отметить, что реологические модели, полученные обоими путями -фиг, 11 и 5, 12 и 6, 13 и 7, несмотря навнешнее различие эквивалентны друг к другу, т.е. описываются идентичными уравнениями,Совпадение температурных режимовявляется определяющим для корректнастдсравнения экспериментальных данных,полученных на разных образцах вязкоупругих сред, изменяющих свои параметры оттемпературы, Кроме того, новая методика,особенно с использованием табл. 1, позволяет практически сразу определить вид реологических моделей и одновременно ихпараметры, а также уравнения состояниядля двух других оставшихся вне экспериментов видов нагружения материала. Данная методика полчения реологическихмоделей и значений их вязких и упругихпараметров необычайно проста в практиче-ском применении, поскольку базируется на 88460 14наиболее удобных и доступных, с точки зрения свойств материала и аппаратурного обеспечения, двух, выбираемых экспериментатором, видах нагружения и исключает проведение дополнительных экспериментов.Впервые решена техническая задачаопределения комплекса реологических параметров линейных вязкоупругих сред при основных четырех видах Однородного нагружения, включая случай одноосного нагружения, выполнение которого прямым путем неосуществимо, например для жидких сред, как и получение коэффициента поперечной деформации для них,Способ позволяет экспериментальными расчетным путем строго установить конкретный вид обобщенного закона Гука для линейных вязкоупругих сред: Рбмк+Я-Р)б= 26 ЦЕ, (ИТ- - 0 а)8 фС 58)Где(э компоненты девиаторного тензоранапряжений,(з - компоненты шарового тензора напряжений,Е; - компоненты девиаторного тензорадеформаций.Як - компоненты шарового тензора деформаций,8; - символ Кронекера.1,) 1=1,2,3параметры которого определяются по вышеизложенной методике.До сих пор вид закона Гука для данныхсред принимался гипотетически из общихсоображений, без строгого эк:периментального обоснования, Знанре обобщен 40 ного закона Гука позволяет решзть любые,в том числе трехмерные, задачи деформирования материала,П р и м е р. Для осуществления одномерного нагружения брали газобетонную смесьследующего состава:портландцемент М 400 - 200 , в т.ч. известково-песчаное вяжущее - 130 активности - 800 , в т,ч. алюминиевая пудра ПАП- 6 в,ч, от массы сухих компонентов, разведенная в ПАВ (сульфанол) содержания 50 50 от массы А, и помещали в сосуд одометра,На поверхность смеси устанавливался уравновешенный поршень, имеющий привод кнагрузочному устройству.45 1788460 16грузкой, мгновенного разгружения матери-моделей сдвига и одномерного нагружения,ала. Перемещения поршня и рост рассчитали искомые параметры и их изметемпературы смеси фиксировались само- нение во времени (фиг. 16, 17, 18, 19) пописцами, На фиг. 1 приведен фрагмент де- экспериментальным данным, приведеннымформационной кривой с участками нафиг,14 и 15(Цифровые расчетыопущены,ползучести вспучивающейся смеси под дей- приведены в графической форме результаствием нагрузки (а 1 - а 2) и участками обрат- ты расчета).ной ползучести при снятии нагрузки(Ь 1- Ь 2), В рассмотренном примере полученыДля осуществления сдвигового нагру- реологические модели и параметры наибожения газобетонная смесь того же состава лее сложных - вспучивающихся, твердеюпомещалась в кювету прибора Вейлера-Ре- щих линейных вязкоупругих сред,биндера, Кювета устанавливалась в сосуд изменяющих свои свойства как от темпераследящего жидкостного термостата, при туры, так и во времени.этом кривая роста температуры смеси, фик- Применение заявляемого способа посируемой термопарой, с помощью следя- зволяет получить весь комплекс реологичещей системы доводилась до совпадения, в ских параметров линейных вязкоупругихпределахзаданногокоридораотклонения, с сред, используя вместо четырех приборовкривой роста температуры смеси при испы- только два, причем наиболее удобных с точтаниях в сосуде одометра, выдерживая, та- ки зрения обращения с материалом, или иским образом, достаточно близкий ходя из вОзйожности лабораторноготемпературный режим смеси при испытани- обеспечения, что приводит к сокращениюях в разных приборах, материальных затрат; кроме того, проведеСдвиговое нагружение смеси по стан- ние двух экспериментов вместо четырехдартной методике осуществлялось с по- значительно сокращает трудозатраты.мощью .уравновешенной рифленой . ф о р мул а и з о б р е те н и япластинки, В качестве режима нагружения Способ определения реологических патакже использован режим периодического раметров линейных вязкоупругих сред примгновенного нагружения постоянной сдви-четырех видах однородного нагружения пуговой нагрузкой, выдержки под нагрузкой, тем снятия кривой ползучести и определемгновенной разгрузки материала. Переме- ЗО ния реологических параметров расчетнымщение пластинки при этом также фиксиро- путем, о т л и ч а ю щ и й с я тем, что, с цельювалось самописцем. повышения информативности, снимают двеНа фиг, 2 приведен фрагмент деформа- кривые ползучести в идентичных темперационной кривой с участками сдвиговой пол- турных условиях при двух различных видахзучести вспучивающейся смеси под З однородного нагружения, определяют реодействием нагрузки (с 1- с 2) и участками об-: ,логические параметры для данных видов наратной ползучести при снятии нагрузки гружения, а реологические параметры для(О 1 - 12), двух других способов нагружения оп ределяБез учета вспучивания деформацион- ют иэ соотношенийное поведение смеси как в условиях одно Оллмерного деформирования (фиг. 1), так и в л (ЗМ - ,4 От)условиях сдвига (фиг. 2) аппроксимирова- е -- луг -лась с достаточной степенью точности моделею стандартного лннелного у= а гд;:но,-,вязкоупругого тела (фиг. 3, 4). Далее с по-, ." вЕч=мощью стандартной методики для каждогоцикла нагружения по кривым ползучести где К = К Т/В -оператор всестороннегорассчитаны упругие и вязкие параметры мо- нагружения;делей (М 1, М 2, , 61, С 2, Я ), Изменение М = М О/С - оператор одномерногоуказанных параметров от цикла к циклу по- нагружения;зволило построить кривые кинетики данных 5 О (3 = 0 . О/Р - оператор сдвигового на-параметров в процессе вспучивания и на- гружения;чального структурообразования смеси (фиг, Е = Е . В/А - оператор одноосного на 14, 15), гружения;Подобрав для случаев всестороннего Е = Е Н/Р - оператор поперечнойнагружения и одноосного нагружения рео деформации;логические модели (фиг. 5, 6, 7) и выразив У - вязкоупругий коэффициент попепараметры указанных моделей, а также па- речной деформации;раметры коэффициента поперечной дефор- А, В, С, О, Е, Й, Р, О, В, Т - линейныемации через параметры реологических дифференциальные операторы вида;5 Г- реологические параметры вязкоупругой среды. 1 о, 11, т 2, , тг. 10 2 оА:а -а - +а - +" +а