Способ обнаружения ошибок при передаче и обработке арифметической информации
Похожие патенты | МПК / Метки | Текст | Заявка | Код ссылки
Текст
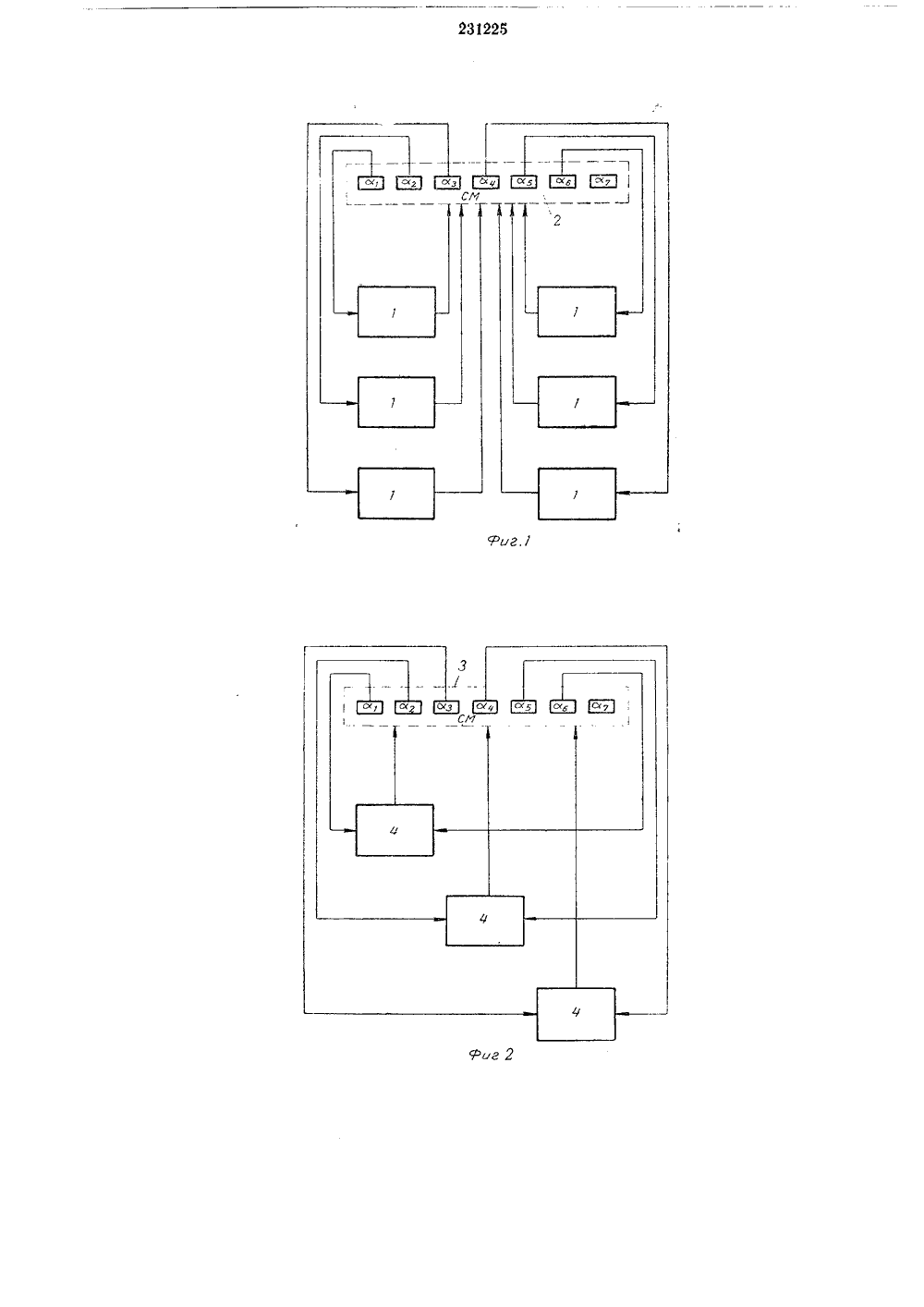
Сова Советскию Сокиалистичевик Республикг л ч-,ависимое от авт. свидетельства42 птеч 14 Заявлено 14 ЛХ.1965 ( 1027411/26-24)с присоединением заявкиПриоритет М 11 К б 061ДК 681 142(088 8) Комитет по делам аобретений и открытий при Совете Министров СССРубликовано 15.Х 1,1968, Бюллетень35та опубликования описания 3.1 Ч,1969 Авторы зобретения кушский и Д, И. Г. Юдицкий Заявите ПОСОБ ОБНАРУЖЕНИЯ ОШИБОК ПРИ ПЕРЕДАЧЕ И ОБРАБОТКЕ АРИФМЕТИЧЕСКОЙ ИНФОРМАЦИИ обнаружеетпческой вычисли- систему ого разрянная для олировать быточных ов полновных прачасть коконтроля ак и для ифметичедиапазонставляетс Известны способы обнаружения ошибок при передаче и обработке арифметической информации в цифровых вычислительных машинах, использующие систему остаточных классов с избыточным кодированием информации.5Предлагаемый способ отличается тем, что вводят дополнительное основание, превышающее любое из оснований рабочего диапазона, оперируют над числами, представленными рабочими цифрами и дополнительной цифрой, по 10 первой цифре конечного результата выбирают из запоминающего устройства константу, такую, чтобы в результате вычитания получить нуль в данном разряде, по следующей цифре первой разности выбирают вторую константу, 15 такую, чтобы в результате вычитания получить нуль во втором разряде, продолжают процедуру вплоть до предпоследней цифры, причем, если в результате вычитания образуются нули правее обрабатываемого разряда, 20 переходят к обработке следующей цифры за последним нулем. Если в результате последняя цифра равна нулю, то ошибки не было, если результат не равен нулю, формируют сигнал ошибки. Это позволяет ускорить обна ружение ошибок и уменьшить оборудование.Для дальнейшего ускорения обнаружения ошибки выбирают константы, анализируя по две крайние цифры г-ую и (п - с)-ую на -ом шаге процедуры, причем переходят к анализу 3( + 1) и (и - т - 1) цифр, если обравны нулю, и формируют сигналесли результат не равен нулю.На фиг. 1 представлена системания ошибок при передаче и арифмобработке информации в цифровыхтельных машинах, использующаяостаточных классов с анализом однда; на фиг. 2 - схема, предназначеанализа двух разрядов.Данный способ позволяет контрЦВМ на основе непозпционных изкодов в системе остаточных классстью арифметичных, в которых на равах участвуют в операциях основнаяда и избыточная, пригодные как дляпередачи числовой информации, тконтроля результата выполнения арских операций.Рассмотрим систему остаточных классов свзаимно-простыми основаниями Р (Р.((Р.В этой системе любое число Л изО, Р), где Р = РРг Р, предвиде Л=(ат,аг, ата,), (2) де а, - остаток от деления числа Л на осноание РВведем дополнительное основание Рл 1.1,взаимно-простое с любым Р, из (1) и удовлетворяющее условиюРл.)) Р ( = 1, 2 и),и будем представлять числа в этой расширенной системеА = (аь а ар, , ал, алл). (3)Это значит, что мы будем представлять числаи производить операции над числами, лежащими в более широком диапазоне (О, Р), гдеР = Рл+1 (4)Так как считаем рабочим диапазоном, т. е.диапазоном, в котором лежат обрабатываемые числа и результаты операций над ними(О, Р), то, очевидно, если на каком-либо этапеобработки оказывается, что числа А ) Р, значит произошла какая-либо ошибка при обработке. Будем числа меньше Р называть правильными, а больше Р - неправильными.Имеет место следующая теорема, которую мыприведем без доказательства,Теорема 1ПустьА,= (а 1, а, , а 1-1, 51, а-)1, , л)1) ( )(5=0,1,2 Р )означает последовательность Р, чисел, у которых цифры по всем основаниям, кроме Родни и те же, а цифры по основанию Р, принимают значения О, 1 Р 1. Тогда в каждом из интервалов=р(+1) - 1) (=0,1, Р ) (6)находится по одному числу этой последовательности, Из этой теоремы вытекает важноеследствие.Следствие. Существует только одно значение 5, =5, при котором число А лежит вР 1интервале (О, - .Р )Действительно, так как в каждом из интервалов 1 имеется по одному числу последова.)тельности А то одно из них попадает в инРтервал 10 = О, - . Основную роль, определяющую свойства введенной системы кодирования, играет вытекающая из предыдущеготеорема.Теорема 2Пусть Р 1РРРл+1 иА = (а 1,аг, , а ал, ал+1) -правильное число.Тогда числоА= (аь аь ., афа , ял ал.)является неправильным.ДоказательствоПравильность числа А означает, чтоР Р РА (, но так как - ) (равенство поРл)л+Рлучается, когда= и + 1), то подавноА . - ,1Следовательно, А находится в интервалеО, - ). В соответствии со следствием предыРР,)дущей теоремы, коль скоро а фа, число А231225 55 60 65 5 10 15 20 25 30 35 40 45 50 4Рне может находчться в интервале О, - , иРво всяком случае А) - , а тогда АР, Рл)т. е. А - неправильное число,Таким образом, данной теоремой устанавливается весьма важный факт для построения обнаруживающей ошибку системы в остаточных классах, а именно: любое искажение цифры по одному какому-либо разряду превращает это число в неправильное и тем самым позволяет обнаружить искажение. Более того, показано, что существует единственное значение этой цифры, которое может превратить неправильное число в правильное. Легко заметить, что теорема доказана в предположении, что введенное дополнительно основание больше любого из оснований системы, что и определяет правило выбора контрольного основания Р+1,Тем же путем можно установить несколько более сильный факт. Пусть среди оснований Р есть такие малые основания Р Р , ,Р ЧтО Р, Р, Р, = Р,(Рл+1. ТОГда любые искажения в цифрах по некоторым или даже по всем этим основаниям превращают правильное число в неправильное, и, следовательно, во всех этих случаях искажения могут быть установлены. Действительно, произведение этих оснований Р можно рассматривать как одно основание, и поскольку соблюдено условие теоремы РРл.).1 будет верно и ее утверждение. Любое же искажение цифры по сснованию Р,может затронуть цифры по нескольким или даже по всем входящим в Р, малым основаниям.Итак, чтобы обнаружить наличие или отсутствие ошибки в числе А, надо сопоставить его с числом Р. Если А )Р, значит имела место сшибка, по крайней мере, в одной цифре,Рассмотрим некоторые примеры, Для этого г,римем систему оснований Р) = 2, Р = 3, Р = 5, Р == 7. Диапазон правильных представлений составляет Р = 2 357 = 210, Вводится контрольное основание Р, ,= 11. Полный диапазон составляет 21011 = 2310. Приведем ортогональные базисы системы: В,= (1,0,0,0,0) =1155 В= (0,1,0,0,0) = = 1540; Вз = (О, О, 1, О, 0) =. 1386; В 4 = = (О, О, О, 1, 0) = 330; В; = (О, О, О, О, 1) = = 210. П р и м е р 1. Вместо правильного числа А = (1, 2, 2, 3, 6) = 17, получено число А =5ошибка, Пропллюстрируем тот факт, что по основанию Р =- 7 при фиксированных цифрах по остальным основаниям только цифра 3 дает правильное числа. Действительно, вычисление других взаимных значений дает(1, 2,2,0, 6) =1337)210; 1, 2,2,1,6) --- = 16667, 210; (1. 2, 2, 2, 6) = 1997 ) 210; (1, 2, 2, 4, 6) =- 347 ) 210 и (1, 2, 2, 6, 6) = = 1007 ) 210.П р и м е р 2, Вместо того же правильного числа А = (1, 2, 2, 3, 6) = 17 получено числоА = (1, 2, 2, 3, 0) - искажена цифра по контрольному основанию.Вычисляем величину А:А = 1.1155+2.1540+2.1386+3.330+ 0,210 -г 2310 в -7997 в .2310=7997 - 6930= 1067)210.Таким образом, А ) 210 - обнаруженаошибка. Этот пример наглядно демонстрируетравноправность контрольнога основания совсеми прочими основаниями. Наличие ошибкиодинаковым образом устанавливается как приошибочной цифре по основанию из рабочегодиапазона, так и при ошибочной цифре поконтрольному основанию.Пример 3. Вместо того же правильногочисла А = (1, 2, 2, 3, 6) = 17 получено числоА = (О, 2, 3, 3, 6). Здесь искакенио подверглись цифры по основаниям 2 и 5. ПосколькуР = 25=10 ( Р; = 11 эта искажение должно быть обнаружено. ДействительноА = 0.1155+2.1540+3.1386 + 3.330 + 6.210 -г 2310 =9488 - 4,2310 =-9488 - 9240 =-248)210.Итак, А - неправильное число.Таким образом, одиночную (в цифре по одному основанию) ошибку всегда можно установить проверкой числа на его вхождение вдиапазон (О, Р). Таким же путем в большинстве случаев мажет быть установлено наличиеошибки и более сложного характера, затрагивающей 2, 3 и более оснований.В ЦВМ в системе остаточных классов ввидуполной независимости работы по к ажломуоснованию наиболее вероятна возможностьошибки именно по одному основанию. Вероятность одновременной ошибки по двум и болееоснованиям на несколько порядков меньшевероятности одиночной ошибки. Поэтому изложенный способ обнаруживает наиболее вероятную ошибку,В приведенных примерах неправильностьвыясняли вычислением значения числа по ортогональным базисам системы, В ЦВМ в системе остаточных классов этот путь неосуществим, так как предполагает вычисления в позиционной системе. Здесь может быть предложен излагаемый далее, легко реализуемый востаточных классах способ.Имеется набор констант С С Спредставляющих собой числа следующего вида:С" = (ц, Ьэи-ц) ц = 112, , Р - 1Сз = (О,Ьз, зз и+ ю) зз = 1,2 Ръ - 15 10 15 20 25 30 35 40 45 50 55 60 65 6Сз" = (О, О, зз, .п-.з) зз = 1,2 Рз - 1 С = (Оэ Оз Оз, О,пэв п;и)=1 ь 2 фэР - 1 С = (О, О, О, О, 4 п Еп-, и) пп =1,2 Р - 1 Общее количество констант составляет Р, + + Р +, , Р - и = М, Процесс проверки на правильность числа А протекает в следующие а шагов (этот процесс мы назовем нулевизацией).1. Вычисляется оазность А=А - С (0,5 з, 5; 5, 5 п+ ) - обращается в нуль цифра первого разряда (С - константа из набора С", у которой 1= а) .иГ2. Вычисляется разность А = А, - С ф =2 = (О, О, 5 54 5 5,) - обращаетз ся в нуль цифра второго разряда (С- константа из набора Сз", у которой 1. = 5 п.зпи - 1 Вычисляется разность А = Аи- С " (О, О,иО, , О, 5,",+) - обращается в нуль цифраи и-го разряда.(Сап - константа из набораиС, у которой 1, = 5"п ) .пЕсли 5"+ = О, то число А неправильное.Примечание, Если на каком-либо у-ом шаге получился результат, у которого, помимо полагающихсянулей слева, содержится нуль и на + 1-ам разряде, то + 1-й шаг пропускается, и производится+ 2-й шаг.Проиллюстрируем способ нулевизаппп примером. Система оснований та же, что в прелыдущих примерах. Паивелем набор констант: 1+2+4+6=13 константС = (1, 1, 1, 1, 1)Сз = (О, 1, 4, 4, 4); Ср =- (О, 2, 2, 2, 2)Сз =- (О, О, 1, 6, 6);Сз = (О, О, 2, 5, 1):Сз= = (0,0,3,4,7);Сз =- Г 0,0,4,3,2)С 4= (0,0,0,1,101;С 4 -- (О, 0,0,2, 8);С 4:(О, О, О, 3, 7); С 4 = (О, О, О, 4, 5)С 4= (0,0,0,5,4);С 4 = (0,0.0,6,2).П р и м е р 4. Проверить на правильность число А = (1, 2, 2, 3, 6).1-й шаг 41 = А - С = (1, 2, 2, 3, 6) - (1, 1, 1, 1, 1) =(О, 1, 1, 2, 5)2-й шаг Аз =- А - Сг= (О, 1, 1, 2, 5) - (О, 1, 4,4,4)=(0,0,2,5,1)3-й шаг Аз -- Лз - Сз= (О, О, 2, 5, 1) - (О, О, 2, 5, 1) =(О, О, О, О, 0)Согласно примечанию 4-й шаг пропускается. Получено 5 з= О, Числа А = (1, 2, 2, 3, 6) - правильное.П р и м е р 5. Проверить на правильность число А = (1, 2, 2, 3, 0).1-йшагА =А - С= (1,2,2,3,0) - (1,1,1, 1, 1)=(0, 1, 1, 2, 10)2-й шаг Аз =- А, - Ся = (О, 1, 1, 2, 10) - (О, 1, 4, 4, 4) = (О, О, 2, 5, 6)231225 Л- -и шаг.2 2О, 5 и.1Обращение в нуль цифр по основаниям Р 2 из набора30 ае 40 2 1, 1, О, 4, О, 3, 2, 1, 2, О, 1, 3,1 1 0 (О, О, О, О, 0) (О, 1, О, О, 4) (О, 2, О, О, 7) 73-й шаг Аз == Аа - Сз= (О, О, 2, 5, 6) - (О, О, 2, 5, 1) =(О, О, О, О, 5)44-й шаг пропускается, Получено 51= 50. Число А = (3, 2, 2, 3, 0) - неправильное. При 5 его получении имела место ошибка.Как видно, способ нулевизации требует п шагов (и - количество оснований рабочего диапазона). Число шагов можно уменьшить вдвое, ведя нулевизацию по двум разрядам в 10 один шаг. Это требует большого запаса констант. Установлено, что наименьшее число констант при парной нулевизации будет, если объединять в нулевизируемые пары разряры Р 1 и Рп, Рг и Р, 1 и т, д. Набор констант в 15 этом случае состоит из РРи+ Р 2 Р 1Ри2 ";1 констант, являющихся наименьшими возможными числами следующего вида:1 и 20 С 1 и - ( а, 1 п 1 п+1)з11 - О, 1, 2 Р, - 1; 1 и -- О, 1, 2, , Рп - 1гп - 1С 2 и - 1: (О 1 аа 1 аа. 12 п 1, 0 12 п 1);исаа=О, 1, 2 Р, - 1;гп - 1 : О, 1, 2 .,Рп1;п и и п., 1 п л,0,02 2 2=0,1, ,Р, - 1.2 2 2Процесс нулевизации числа А в этом случсостоит из следующих - шагов:21-й шаг. Вычисляется разность А 1 п = АС 1 п: (О, 52, 5 з,.5 п - 1 0 5 л+1)Обращение в нуль цифр по основаниям Р,0 (О, О, О, О, 0) (1,1 (О, 2, 3, 1, 8) (1,2 (О, 2, 2, 2, 2) (1,3 (О, 1, О, 3, 1 О) (1,4 (О, 1, 4, 4, 4) (1,5 (О, О, 2, 5, 1) (1,6 (О, О, 1, 6, 6) (1,о 1 (О, О, 1, О, 5) (О, 1, 1,2 (О, О, 2, О, 9) (О, 1, 2, 3 (О, О, 3, О, 3) (О, 1, 3, 4 (О, О, 4, О, 7) (О, 1, 4,П р и м е р 6. Провсрпть правильность числа А = (1, 2, 2, 3, 6) способом парной нулевизации. 45 1-й шаг: А, = А - С 4 (1, 2, 2, 3, 6) - (1, О, 3, 3, 3)=(0, 2, 4, О, 3) 8"Рп л 1 пРи(Сги - константа из набора Сы, у которой 11 = а, 1 ып= ап)2-й шаг, Вычисляется разносгь Аг,- Аив - С 2 п - 1: (О, О, 5 з5 л - 2, 0 О 5 пз 1 ).Обращение в нуль цифр по основаниям Рг и2 л - 1 гп - 1 Рп 1 (С ,"- - константа из набора Сгп у Которои гаа: 52 12 п 1: 5 п 1)- " - 1 г г Вычисляется разность 5 п 5Апп =Ап и - Слл =О 00 2 2 2 2 2 2 Р л /Сл - константа - +1-- +1 22 2 Если теперь 5, + О, то число А неправильное.Здесь можно сделать аналогичное примечание о пропуске соответствующего шага, если цифры по обоим нулевизируемым на этом шаге разрядам уже оказываются нулями в результате выполнения предыдущего шага.Приведем иллюстрирующий пример. Составим необходимые константы для парной нулевизации по основаниям (2, 7) - первая пара и (3, 5) - вторая пара.О, 7)1, 1)2, 9)3, 3)4, 0)5, 5)6, 2) О, 9) (О, 2, 1, О, 1)О, 2) (О, 2, 2, О, 6)О, 6) (О, 2, 3, О, 10)О, 0) (О, 2, 4, О, 3)2-й ш аг: Ааз = А,4 - Сгз = (О, 2, 4, О, 3) -24проникнуть необнаруженная ошибка, посколь ку это могло бы произойти только в том случае, когда результат вычислений был бы правильньв, но в то же время не истинным числом. Согласно же данной теореме как раз этого быть не может.Таким образом, ошибка, если она на каком- либо этапе реализации вычислений по цепи операций имела место, либо сохранится до конца вычислений и проявит себя легко обнарукиваемой указанным выше способом неправильностью конечного результата, либо в процессе дальнейших после своего возникновения вычислений самоустранится, и тогда будет получен нужный конечный результат.Самоустранение ошибки может произойти как при налокении нескольких сбоев по данному основачию, так и при одиночном сбое. Например, если на каком-либо этапе вычислений по цепи операций уже после возникновения сбоя по основанию Р, промежуточный результат умножался на число, имеющее нулевую цифру по основанию Р, то, очевидно, произведение получится истинным числом и таковым уже войдет в последующие вычисления, что при отсутствии в дальнейшем сбоев, естественно, приведет к получению истинного конечного результата.Возможность при данной системе обнаружения ошибок проверять только выходные конечные результаты цепи операций эквивалентна по своему эффекту выполнению второго просчета. Такой режим работы цифровой вычислительной машины повышает ее эффективную производительность в два раза.Рассмотрим практическую реализацию устройств для обнаружения ошибок,Пусть арифметическое устройство предназначено для работы в диапазоне представления чисел (О, Р) = (0,10 з). Для реализации указанного диапазона может быть выбрана система остаточных классов с основаниямиР, = 17 Р = 19 Рз = 23 Р 4 = 27 Р- = 29Р 6Введем дополнительно контрольное основание Р, = 32, взаимно-простое с выбранными рабочими основаниями. Число А в этой системе представляется в виде А = (аь аз, аз а 4, аз, а, а 7). Тогда для обнаружения ошибки в цифре отдельного основания может быть предложено несколько способов.Способ 1. Поскольку анализировать число на правильность можно не при каждой операции, а после целого этапа расчетов, то практически без уменьшения производительности ЭВМ указанный анализ может производиться программным методом,В накопителе вычислительной машины разместим таблицу для нулевизации в соответ 65 числа А = (О, 2, 3, 3, 6) способом парной нулевизации,1-й шаг: А= А - С 4 =- (О, 2, 3, 3, 6) - (О, 1, О, 3, 10) =(О, 1, 3, О, 7)тз2-й шаг: А.з = А - Сгз = (О, 1, 3, О, 7) -- (О, 1, 3, О, 6) = (О, О, О, О, 1).2Ь = 170. Число А - неправильное. При. его получении имела место ошибка,Таким образом, предложенные способы позволяют обнаружить ошибку в кодовом слове (числе), независимо от того, возникла эта ошибка при передаче информации или при ее обработке в арифметическом устройстве ЦВМ в системе остаточных классов.Для предлагаемой системы обнаружения ошибок характерно следующее весьма важное обстоятельство. Указанную проверку на правильность вовсе не надо производить над каждым кодовым словом, возникающим при каждом выполнении элементарной операции в ЦВМ. Напротив, этой проверке надо подвергать только результаты вычислений по отдельным этапам, являющихся ответными, выходными результатами, не носящими промежуточный характер. Объем этапа и частота проверки определяются в каждой реализуемой на ЦВМ программе индивидуально, в соответствии с особенностями программы. Возможность такого режима реализации контроля, который значительно повышает эффективность предлагаемой системы обнаружения, основывается на следующей теореме.Теорема. Пусть выполняется некоторая цепь рациональных операций, результат которых (истинный), в случае отсутствия ошибок в ходе вычислений, должен быть правильным числом и пусть в процессе вычисления имел место один или несколько сбоев по одному из оснований системы. Тогда конечный результат вычислений по цепи либо неправильный, либо истинный.Действительно, пусть истинным результатом вычислений по цепи операций должно быть число К =- (к, к, , к+), а получено число А = (а, и а, ап+)Если сбой имел место по основанию Р то а, = х а,: х аС= х , ае+у = хс+т р хд зз п+1 хл+1Что касается а то возможны два варианта: 1) афх и 2) а - х,В варианте 1, согласно теореме 2, число А неправильное. В варианте 2 число А правильное и при этом совпадающее с К, т. е. А является истинным значением конечного результата цепи.Установленный, казалось бы, весьма простой факт важен для построения системы обнаружения ошибок в цифровой вычислительной машине в системе остаточных классов. Он свидетельствует о том, что в конечный результат вычисления по цепи операций не може 5 10 15 20 25 30 35 40 45 50 55 60 ствии с адресами (аь аз), (аз, а 5), (аз а 4)Обращаясь последовательно по этим адресам в накопитель и складывая (вычитая) полученные оттуда константы с исходным числом, мы всю операцию нулевизации выпол5 10 15 няем за три сложения с последующим анализом на О и выработкой признака в такого, что1, если результат нулевойа= илиО в остальных случаях.Если в результате проверки окажется, что а = О, это значит, что имела место ошибка, а передачей управления по о мы можем перевести ЭВМ в режим исправления ошибки. При этом способе в ЭВМ никакие дополнительные цепи для обнаружения ошибки не вводят. Операция обнаружения занимает три рабочих такта сложения (вычитания), а для хранения констант в накопителе ЭВМ должно быть зарезервировано Р,Рв + РРв+ РвР 4 рабочих ячеек. В нашем случае требуется 1731+ 1929+23 27=1699 ячеек, т. е. при отсутствии дополнительного оборудования требуется занять довольно большой участок емкости накопителя.Способ 2, Тот же программный метод может быть приложен к непарной нулевизации. По значению каждой цифры (рассматривая ее как адрес) а, а., ав, а, ав, а, последовательно находим константу нулевизации и складываем (вычитаем) ее с остатком исходного числа. Результат проверяем на нуль. При этом потребуется выполнить шесть операций сложения (вычитания), В накопителе требуется зарезервировать под константы Р 1 + Р, + Рв + Р + Рв + Рв = 17+19+23+27+29+31 = 146 ячеек, т. е. вместо трех операций нулевизации требуется выполнить шесть операций, но зато количество требуемых ячеек накопителя сокращается более чем в десять раз, Нестандартного оборудования не требуется.Способ 3. Нулевизация проводится последовательно по цифрам а, а, ав, а 4, ав,ав с анализом результата на нуль. Константы нулевизации закоммутированы в регистрах 1 вне накопителя (см, фиг. 1).По значениям цифр числа, хранящегося в арифметическом устройстве 2, производится последовательное обращение за константами нулевизации и их последовательное сложение (вычитание) с остатком от исходного числа. По цифре а, мы выбираем константу а имеющую все цифры, кроме аь и складываем с исходным числом, По цифре а выбирается константа а, имеющая цифры ав, ав, а;, ав, а 7, и складывается с числом из устройства 2. По цифре а, константа состоит из цифр а 4, а;, ав, а 7. По цифре а складываем с содержимым сумматора число с цифрами а;, ав, и 7. Полученная цифра ав определит константу а 1 с го 25 зо 35 40 45 50 55 цифрами ав и а 7. И, наконец, полученная цифра ав определит константу для разряда а 7.После выполнения указанной процедуры анализируем на О цифру а,. Ее не нулевое значение говорит о наличии ошибки, нулевое - об отсутствии,Указанный способ требует нестандартного оборудования, однако места в оперативном накопителе под константы не требуются, а в оборудовании учитывается последовательное уменьшение разрядности констант.Способ 4. Тот же метод, что и в способе 3, может быть использован для парной нулевизации, Устройство (фиг. 2) при этом содержит арифметический регистр 3 и регистры констант 4, выбираемых по а, и в г. Предмет изобретения1. Способ обнаружения ошибок при передаче и обработке арифметической информации в цифровых вычислительных машинах, использующий систему остаточных классов с избыточным кодированием информации, отличаюи 1 ийся тем, что, с целью ускорения процедуры обнаружения ошибок и уменьшения требуемого оборудования, вводят дополнительное основание, превышающее любое из оснований рабочего диапазона, оперируют над числами, представленными рабочими цифрами и дополнительной цифрой, по первой цифре конечного результата выбирают из запоминающего устройства константу, такую, чтобы в результате вычитания получить нуль в данном разряде, по следующей цифре первой разности выбирают вторую константу, такую, чтобы в результате вычитания получить нуль во втором разряде, продолжают процедуру вплоть до предпоследней цифры, причем, если в результате вычитания образуются нули правее обрабатываемого разряда, переходят к обработке следующей цифры за последним нулем, причем, если в результате последняя цифра равна нулю, то ошибка не имела места, если результат оказывается не равным нулю, формируют сигнал ошибки.2. Способ по п. 1, отличающийся тем, что, с целью дальнейшего ускорения процедуры обнаружения опибки, выбирают константы, анализируя по две крайние цифры -ую и (и -- ) -ую на км шаге процедуры, причем переходят к анализу (+ 1) и (и -- 1) цифр, если обе цифры равны нулю, и формируют сигнал ошибки, если результат не равен нулю.
СмотретьЗаявка
1027411
И. Я. Акушский, Д. И. Г. Юдицкий
МПК / Метки
МПК: G06F 11/08
Метки: арифметической, информации, обнаружения, обработке, ошибок, передаче
Опубликовано: 01.01.1968
Код ссылки
<a href="https://patents.su/7-231225-sposob-obnaruzheniya-oshibok-pri-peredache-i-obrabotke-arifmeticheskojj-informacii.html" target="_blank" rel="follow" title="База патентов СССР">Способ обнаружения ошибок при передаче и обработке арифметической информации</a>
Предыдущий патент: Запоминающее устройство на цилиндрических магнитных пленках
Следующий патент: Аналоговая вычислительная машина с непрерывным диагностическим контролем
Случайный патент: Способ и устройство для разделения тутового шелкопряда по полу на стадии бабочек